Wideband beam-steerable reflectarray with polarization-rotating unit cells#
This example demonstrates how to design and optimize a wideband reflectarray based on polarization-rotating unit cells (PRUCs) using Tidy3D. The design is based on the work by Luyen et al., where a reflectarray design is demonstrated with wide bandwidth and beam-steering capabilities using minimum-switch topology.
The design consists of:
A polarization-rotating unit cell (PRUC) with two configurations (0° and 180° rotation)
Arrow-shaped metallic patches on the top layer
Ground plane with circular holes in the middle layer
Bottom layer with diagonal connecting strips, which enable the switching behavior
Rogers RO4003C substrate layers bonded by Rogers RO4450B prepregs

Key features:
Full-wave electromagnetic simulation of the unit cell using periodic boundary conditions
Optimization of geometric parameters using Bayesian optimization
Analysis of reflection coefficients and fractional bandwidth
Cell designs achieving over 58% fractional bandwidth for cross-polarized reflection
This notebook shows how to:
Create parametric geometry for the PRUC design
Set up periodic boundary conditions and plane wave excitation
Configure optimization of key geometric parameters
Analyze reflection coefficients and bandwidth performance
Let’s start by importing the required packages and defining some basic parameters.
[1]:
# standard python imports
from copy import copy
from typing import Union
import matplotlib.pyplot as plt
# additional imports to aid in geometry processing and post-processing of results
import numpy as np
import pandas as pd
import shapely as shapely
# tidy3d imports
import tidy3d as td
# design plugin for performing the Bayesian optimization of the PRUC
import tidy3d.plugins.design as tdd
import xarray as xr
# dispersion plugin for fitting loss tangent to complex-conjugate pole-residue pair model
from tidy3d.plugins.dispersion import FastDispersionFitter
[2]:
# Frequency range of interest is 8 to 12 GHz
freq_start = 4e9
freq_stop = 16e9
# Center frequency of 10 GHz
freq0 = (freq_start + freq_stop) / 2
fwidth = 9e9
# Center wavelength
wavelength0 = td.C_0 / freq0
# Longest wavelength
wavelength_start = td.C_0 / freq_start
freqs = np.linspace(freq_start, freq_stop, 101)
wvl_um = td.C_0 / freqs
run_time = 20e-9 # 20 ns run time
# Tidy3D uses microns by default
mm = 1e3
# Default unit cell parameters
S = 6 * mm # size of the unit cell
s = 0.15 * mm # spacing between arrow and unit cell boundary
l_stem = 2.7 * mm # length of arrow from via center to tip
l_head = 2.75 * mm # length of arrow head
w_stem = 0.25 * mm # width of arrow stem
w_head = 0.7 * mm # width of arrow head
d_via = 0.46 * mm # Via diameter
w_cnx = 0.5 * mm # Width of connector on bottom layer
# Custom parameters not given in [1]
w_via_pad = 0.5 * mm # Width of via pad on the top layer
d_hole = 0.9 * mm # Hole diameter in ground plane
# Substrate is three layers of Rogers RO4003C bonded by two layers of 0.1 mm
# thick Rogers RO4450B prepregs with total thickness 3.35 mm
prepreg_t = 0.102 * mm
l1_t = 0.813 * mm
l2_t = 1.524 * mm
l3_t = 0.813 * mm
structure_t = 2 * prepreg_t + l1_t + l2_t + l3_t
# Used to define grid discretization
dl_xy = 0.1 * mm # resolution in the xy plane
dl_hole = 0.05 * mm # grid resolution around ground plane holes
dl_z = 0.05 * mm # resolution along the z axis
# Metals modeled as 35 microns thick
metal_t = 0.035 * mm
# Substrate material properties
RO4003C_er = 3.4
RO4003C_losstan = 0.0027
RO4450B_er = 3.54
RO4450B_losstan = 0.004
RO4003C = FastDispersionFitter.constant_loss_tangent_model(
eps_real=RO4003C_er,
loss_tangent=RO4003C_losstan,
frequency_range=(freq_start, freq_stop),
max_num_poles=3,
tolerance_rms=1e-3,
)
RO4450B = FastDispersionFitter.constant_loss_tangent_model(
eps_real=RO4450B_er,
loss_tangent=RO4450B_losstan,
frequency_range=(freq_start, freq_stop),
max_num_poles=3,
tolerance_rms=1e-3,
)
# All metals are modeled as perfect electric conductors
patch_metal = td.PEC
# Simulation domain definition with sufficient padding around the structure for PMLs
sim_size = (S, S, structure_t + wavelength_start / 2)
sim_center = [0, 0, 0]
Helper Class Definitions#
In this section, we define two helper classes which simplify the process of constructing the unit cell and reflectarray structure. Since the cells in this section are only needed for defining the Tidy3D structures, mesh overrides, and snapping points, feel free to skip to following section describing the structure setup.
PRUC Geometry#
We define a PRUC (Polarization-Rotating Unit Cell) helper class which creates the fundamental building block of the reflectarray.
The class is initialized by parameters describing the unit cell dimensions (cell size, arrow dimensions, via sizes, etc.)
calc_via_offset()- Calculates where to place the vias in the unit cellmake_single_arrow()- Creates coordinates for one arrow-shaped patchmake_all_arrows()- Creates four rotated copies of the arrow for the unit cellmake_bottom_layer()- Creates the bottom connecting stripsmake_ground_layer()- Creates the ground plane with holesmake_vias()- Creates the connecting vias between layersmake_unit_cell_geometry()- Assembles all components into complete unit cell
The class handles both 0° and 180° rotated versions of the unit cell through the bit_version parameter, which controls the orientation of the bottom layer connections.
[3]:
class PRUC:
"""Class representing a Polarization-Rotating Unit Cell (PRUC) for reflectarray antennas.
This class defines the geometry of a unit cell containing four arrow-shaped patches
connected by vias through a ground plane. The cell can be rotated 0° or 180° to
encode binary phase information.
Attributes
----------
S : float
Size of the square unit cell aperture in microns.
s : float
Spacing between arrow patches and unit cell boundary in microns.
l_head : float
Length of the arrow head in microns.
l_stem : float
Length from via center to arrow tip in microns.
w_stem : float
Width of the arrow stem in microns.
w_head : float
Width of the arrow head in microns.
w_via_pad : float
Width of the square via pad on top layer in microns.
w_cnx : float
Width of the bottom layer connections between vias in microns.
d_via : float
Diameter of the metal vias in microns.
d_hole : float
Diameter of the holes in the ground plane in microns.
metal_t : float
Thickness of all metal layers in microns.
z_top : float
Z-coordinate of top substrate surface (excluding metal) in microns.
z_ground : float
Z-coordinate of ground plane substrate surface in microns.
z_bottom : float
Z-coordinate of bottom substrate surface (excluding metal) in microns.
bit_version : bool
If True, rotates bottom connections 180° to encode binary '1' state.
If False, keeps 0° rotation for binary '0' state.
"""
def __init__(
self,
S: float,
s: float,
l_head: float,
l_stem: float,
w_stem: float,
w_head: float,
w_via_pad: float,
w_cnx: float,
d_via: float,
d_hole: float,
metal_t: float,
z_top: float,
z_ground: float,
z_bottom: float,
bit_version: bool,
):
self.S = S
self.s = s
self.l_head = l_head
self.l_stem = l_stem
self.w_stem = w_stem
self.w_head = w_head
self.w_via_pad = w_via_pad
self.w_cnx = w_cnx
self.d_via = d_via
self.d_hole = d_hole
self.metal_t = metal_t
self.z_top = z_top
self.z_ground = z_ground
self.z_bottom = z_bottom
self.bit_version = bit_version
def calc_via_offset(self):
"""Calculates the offset of the via in the unit cell"""
return self.S / 2 - self.s - self.l_stem / np.sqrt(2)
def make_single_arrow(self) -> list[tuple[float, float]]:
"""Returns the 2D coordinates of a single arrow in the unit cell corresponding with the first quadrant."""
def swap_xy(xy: tuple[float, float]):
"""Applies a reflection along the y = x line."""
return (xy[1], xy[0])
via_offset = self.l_stem / np.sqrt(2)
# Create points along half of an arrow
tr = (0, 0)
br = (0, -self.l_head)
br2 = (-self.w_head, -self.l_head)
in_corner = (-self.w_head, -self.w_head - self.w_stem / np.sqrt(2))
bl = (
-via_offset + self.w_stem / np.sqrt(8),
-via_offset - self.w_stem / np.sqrt(8),
)
# Complete arrow is created by reflecting points across y = x line
arrow_points = [
tr,
br,
br2,
in_corner,
bl,
swap_xy(bl),
swap_xy(in_corner),
swap_xy(br2),
swap_xy(br),
swap_xy(tr),
]
# Use shapely polygon operations to create the union of the arrow and via pad.
arrow = shapely.Polygon(arrow_points)
via_pad = shapely.box(
-via_offset - 0.5 * self.w_via_pad,
-via_offset - 0.5 * self.w_via_pad,
-via_offset + 0.5 * self.w_via_pad,
-via_offset + 0.5 * self.w_via_pad,
)
arrow_shapely = shapely.union(arrow, via_pad)
return arrow_shapely.exterior.coords
def make_all_arrows(self) -> list[td.PolySlab]:
"""Returns a list of all arrows in the unit cell by using rotations and translations."""
slab_bounds = (self.z_top, self.z_top + self.metal_t)
arrow_tr_verts = np.array(self.make_single_arrow())
arrow_tl_verts = np.copy(arrow_tr_verts)
arrow_tl_verts[:, 0] *= -1
arrow_bl_verts = np.copy(arrow_tl_verts)
arrow_bl_verts[:, 1] *= -1
arrow_br_verts = np.copy(arrow_tr_verts)
arrow_br_verts[:, 1] *= -1
corner_offset = self.S / 2 - self.s
arrow_tr_verts += np.array([corner_offset, corner_offset])
arrow_tr = td.PolySlab(vertices=arrow_tr_verts, axis=2, slab_bounds=slab_bounds)
arrow_tl_verts += np.array([-corner_offset, corner_offset])
arrow_tl = td.PolySlab(vertices=arrow_tl_verts, axis=2, slab_bounds=slab_bounds)
arrow_bl_verts += np.array([-corner_offset, -corner_offset])
arrow_bl = td.PolySlab(vertices=arrow_bl_verts, axis=2, slab_bounds=slab_bounds)
arrow_br_verts += np.array([corner_offset, -corner_offset])
arrow_br = td.PolySlab(vertices=arrow_br_verts, axis=2, slab_bounds=slab_bounds)
return [arrow_tr, arrow_tl, arrow_bl, arrow_br]
def make_bottom_layer(self) -> td.Geometry:
"""Returns the bottom layer of the unit cell"""
via_center = self.calc_via_offset()
# Horizontal connections
zcenter = self.z_bottom - self.metal_t / 2
thickness = self.metal_t
strip = td.Box(
center=(0, 0, zcenter),
size=(
2 * np.sqrt(2) * (via_center) + self.d_via + (self.w_cnx - self.d_via),
self.w_cnx,
thickness,
),
)
angle = -np.pi / 4
if self.bit_version:
angle = np.pi / 4
rotate_45 = td.Transformed.rotation(axis=2, angle=angle)
strip = td.Transformed(geometry=strip, transform=rotate_45)
geo_tuple = (strip,)
metal_regions = td.GeometryGroup(geometries=geo_tuple)
return metal_regions
def make_ground_layer(self, ground_width: float = None) -> td.Geometry:
"""Returns the ground layer of the unit cell"""
zcenter = self.z_ground + self.metal_t / 2
thickness = self.metal_t
via_center = self.calc_via_offset()
ground_size = (self.S, self.S, thickness)
if ground_width is not None:
ground_size = (ground_width, ground_width, thickness)
ground = td.Box(center=(0, 0, zcenter), size=ground_size)
hole_size = (self.d_hole, self.d_hole, thickness)
hole_tr = td.Box(center=(via_center, via_center, zcenter), size=hole_size)
hole_tl = td.Box(center=(-via_center, via_center, zcenter), size=hole_size)
hole_bl = td.Box(center=(-via_center, -via_center, zcenter), size=hole_size)
hole_br = td.Box(center=(via_center, -via_center, zcenter), size=hole_size)
holes = td.GeometryGroup(geometries=(hole_tr, hole_tl, hole_bl, hole_br))
ground_with_holes = td.ClipOperation(
operation="difference", geometry_a=ground, geometry_b=holes
)
return ground_with_holes
def make_vias(self) -> tuple[td.Cylinder, td.Cylinder, td.Cylinder, td.Cylinder]:
"""Returns the vias in the unit cell"""
via_center = self.calc_via_offset()
center_z = (self.z_top + self.z_bottom) / 2
length = self.z_top - self.z_bottom
radius = self.d_via / 2
tr = td.Cylinder(
center=(via_center, via_center, center_z),
length=length,
radius=radius,
axis=2,
)
tl = td.Cylinder(
center=(-via_center, via_center, center_z),
length=length,
radius=radius,
axis=2,
)
bl = td.Cylinder(
center=(-via_center, -via_center, center_z),
length=length,
radius=radius,
axis=2,
)
br = td.Cylinder(
center=(via_center, -via_center, center_z),
length=length,
radius=radius,
axis=2,
)
return tr, tl, bl, br
def make_unit_cell_geometry(
self, dl_hole: float, ground_width: float = None
) -> tuple[
td.GeometryGroup,
list[td.MeshOverrideStructure],
list[tuple[float, float, float]],
]:
"""Returns the geometry of the metallic portion of the unit cell,
mesh overrides around the holes, and the vertices of the arrows."""
arrows = self.make_all_arrows()
bottom_geometry = self.make_bottom_layer()
ground_with_holes = self.make_ground_layer(ground_width)
via_geometry = self.make_vias()
all_geometries = tuple(
arrows + [bottom_geometry] + [ground_with_holes] + list(via_geometry)
)
geometry_group = td.GeometryGroup(geometries=all_geometries)
# Make regions of mesh refinement
mesh_overrides = [
td.MeshOverrideStructure(geometry=hole, dl=[dl_hole, dl_hole, self.metal_t])
for hole in ground_with_holes.geometry_b.geometries
]
# Get arrow vertices for snapping points
arrow_verts = [
(vert[0], vert[1], self.z_top) for arrow in arrows for vert in arrow.vertices
]
return geometry_group, mesh_overrides, arrow_verts
PRUC Array Structure Construction#
The PRUCArray class handles the construction of a complete reflectarray antenna by arranging multiple Polarization-Rotating Unit Cells (PRUCs) in a regular grid. It manages:
Assembly of unit cells in an Nx × Ny array configuration
Creation of substrate and prepreg layers
Specification of material properties
Definition of mesh refinement regions
Key methods:
make_substrates(): Creates the layered dielectric structuremake_array(): Constructs the full reflectarray using a binary mask to determine cell rotations
The array construction supports:
Arbitrary array dimensions through
NxandNyparametersExtended substrate areas beyond the unit cell boundaries
Custom mesh refinement around critical features
Material specifications for substrates, prepregs, and metals
[4]:
class PRUCArray:
"""Class representing an array of Polarization-Rotating Unit Cells (PRUCs).
This class handles the construction of a reflectarray consisting of multiple PRUCs,
including substrate layers and mesh refinement specifications.
Attributes
----------
unit_cell_0 : PRUC
Unit cell representing binary '0' state with 0° rotation.
unit_cell_1 : PRUC
Unit cell representing binary '1' state with 180° rotation.
Nx : int
Number of unit cells along x-axis.
Ny : int
Number of unit cells along y-axis.
array_sx : float
Size of array in x-direction in microns. Allows for substrates that extend farther than the unit cells.
array_sy : float
Size of array in y-direction in microns. Allows for substrates that extend farther than the unit cells.
prepreg_t : float
Thickness of prepreg layers in microns.
l1_t : float
Thickness of top substrate layer in microns.
l2_t : float
Thickness of middle substrate layer in microns.
l3_t : float
Thickness of bottom substrate layer in microns.
substrate_medium : Medium
Material properties of the substrate layers.
prepreg_medium : Medium
Material properties of the prepreg layers.
metal_medium : Medium
Material properties of the metal layers.
dl_hole : float
Mesh cell size for refinement around holes in microns.
dl_xy : float
Mesh cell size in xy-plane in microns.
dl_z : float
Mesh cell size in z-direction in microns.
"""
def __init__(
self,
unit_cell_0: PRUC,
unit_cell_1: PRUC,
Nx,
Ny,
array_sx,
array_sy,
prepreg_t,
l1_t,
l2_t,
l3_t,
substrate_medium,
prepreg_medium,
metal_medium,
dl_hole: float,
dl_xy: float,
dl_z: float,
):
self.unit_cell_0 = unit_cell_0
self.unit_cell_1 = unit_cell_1
self.Nx = Nx
self.Ny = Ny
self.array_sx = array_sx
self.array_sy = array_sy
self.prepreg_t = prepreg_t
self.l1_t = l1_t
self.l2_t = l2_t
self.l3_t = l3_t
self.substrate_medium = substrate_medium
self.prepreg_medium = prepreg_medium
self.metal_medium = metal_medium
self.dl_hole = dl_hole
self.dl_xy = dl_xy
self.dl_z = dl_z
def make_substrates(
self,
) -> tuple[list[td.Structure], list[td.MeshOverrideStructure]]:
"""Create the layered substrate structure for the reflectarray along
with mesh overrides that refine the mesh along the normal axis of the layers."""
top_l1 = 0
top_l2 = top_l1 - self.l1_t - self.prepreg_t
top_l3 = top_l2 - self.l2_t - self.prepreg_t
bottom = top_l3 - self.l3_t
metal_t = self.unit_cell_0.metal_t
array_sx = self.array_sx
array_sy = self.array_sy
sub1 = td.Structure(
geometry=td.Box(
center=(0, 0, top_l1 - self.l1_t / 2),
size=(array_sx, array_sy, self.l1_t),
),
medium=self.substrate_medium,
)
prepreg1 = td.Structure(
geometry=td.Box(
center=(0, 0, top_l1 - self.l1_t - self.prepreg_t / 2),
size=(array_sx, array_sy, self.prepreg_t),
),
medium=self.prepreg_medium,
)
sub2 = td.Structure(
geometry=td.Box(
center=(0, 0, top_l2 - self.l2_t / 2),
size=(array_sx, array_sy, self.l2_t),
),
medium=self.substrate_medium,
)
prepreg2 = td.Structure(
geometry=td.Box(
center=(0, 0, top_l2 - self.l2_t - self.prepreg_t / 2),
size=(array_sx, array_sy, self.prepreg_t),
),
medium=self.prepreg_medium,
)
sub3 = td.Structure(
geometry=td.Box(
center=(0, 0, top_l3 - self.l3_t / 2),
size=(array_sx, array_sy, self.l3_t),
),
medium=self.substrate_medium,
)
substrates = [sub1, prepreg1, sub2, prepreg2, sub3]
patch_box = td.Box(center=(0, 0, top_l1 + metal_t / 2), size=(array_sx, array_sy, metal_t))
ground_box = td.Box(
center=(0, 0, top_l3 + metal_t / 2),
size=(array_sx, array_sy, metal_t),
)
bottom_box = td.Box(
center=(0, 0, bottom - metal_t / 2),
size=(array_sx, array_sy, metal_t),
)
dl_metals = (self.dl_xy, self.dl_xy, metal_t)
dl_subs = (self.dl_xy, self.dl_xy, self.dl_z)
substrate_overrides = [
td.MeshOverrideStructure(geometry=patch_box, dl=dl_metals),
td.MeshOverrideStructure(geometry=ground_box, dl=dl_metals),
td.MeshOverrideStructure(geometry=bottom_box, dl=dl_metals),
td.MeshOverrideStructure(geometry=prepreg1.geometry, dl=dl_subs),
td.MeshOverrideStructure(geometry=prepreg2.geometry, dl=dl_subs),
td.MeshOverrideStructure(geometry=sub1.geometry, dl=dl_subs),
td.MeshOverrideStructure(geometry=sub2.geometry, dl=dl_subs),
td.MeshOverrideStructure(geometry=sub3.geometry, dl=dl_subs),
]
return substrates, substrate_overrides
def make_array(
self, bit_mask: Union[xr.DataArray, bool], ground_width: float = None
) -> tuple[
td.GeometryGroup,
list[td.MeshOverrideStructure],
list[tuple[float, float, float]],
]:
"""Returns all Tidy3D structures, mesh overrides and snapping points for the array."""
S = self.unit_cell_0.S
xstart = -self.Nx / 2.0 * S + 0.5 * S
ystart = -self.Ny / 2.0 * S + 0.5 * S
substrate_structures, substrate_overrides = self.make_substrates()
geo_unit_cell_0, cell_overrides, cell_snapping_points = (
self.unit_cell_0.make_unit_cell_geometry(
dl_hole=self.dl_hole, ground_width=ground_width
)
)
geo_unit_cell_1, _, _ = self.unit_cell_1.make_unit_cell_geometry(
dl_hole=self.dl_hole, ground_width=ground_width
)
def get_cell_variant(i, j):
if type(bit_mask) is bool:
return bit_mask
return bit_mask[i, j].item()
unit_cell_geos = []
mesh_overrides = []
arrow_snapping_points = []
for i in range(0, self.Nx):
dx = xstart + i * S
for j in range(0, self.Ny):
dy = ystart + j * S
# Add translated geometries
translate = td.Transformed.translation(dx, dy, 0)
if get_cell_variant(i, j):
transformed_cell = td.Transformed(geometry=geo_unit_cell_1, transform=translate)
else:
transformed_cell = td.Transformed(geometry=geo_unit_cell_0, transform=translate)
unit_cell_geos.append(transformed_cell)
# Add mesh overrides
mesh_overrides += [
override_hole.updated_copy(
path="geometry",
center=(
dx + override_hole.geometry.center[0],
dy + override_hole.geometry.center[1],
override_hole.geometry.center[2],
),
)
for override_hole in cell_overrides
]
# Add snapping points
arrow_snapping_points += [
(v[0] + dx, v[1] + dy, v[2]) for v in cell_snapping_points
]
all_cells = td.GeometryGroup(geometries=unit_cell_geos)
all_cells_structure = td.Structure(geometry=all_cells, medium=self.metal_medium)
all_structures = substrate_structures + [all_cells_structure]
all_mesh_overrides = substrate_overrides + mesh_overrides
return all_structures, all_mesh_overrides, arrow_snapping_points
Setup#
Structure Setup#
Using the helper classes defined earlier, we create an array consisting of a single unit cell, since in this notebook we are interested in optimizing the unit cell design [1].
We plot a candidate unit cell in the figures below.
[5]:
# Positions of the substrate interfaces
top_l1 = 0
top_l2 = top_l1 - l1_t - prepreg_t
top_l3 = top_l2 - l2_t - prepreg_t
bottom = top_l3 - l3_t
substrate_width = 2 * S
unit_cell_1 = PRUC(
S=S,
s=s,
l_head=2.5 * mm, # l1,
l_stem=3 * mm, # l2,
w_stem=w_stem,
w_head=w_head,
w_via_pad=w_via_pad,
w_cnx=w_cnx,
d_via=d_via,
d_hole=d_hole,
metal_t=metal_t,
z_top=0.0,
z_ground=top_l3,
z_bottom=bottom,
bit_version=True,
)
unit_cell_0 = copy(unit_cell_1)
unit_cell_0.bit_version = False
array = PRUCArray(
unit_cell_0=unit_cell_0,
unit_cell_1=unit_cell_1,
Nx=1,
Ny=1,
array_sx=substrate_width, # Make array large enough that the substrates extend passed the simulation boundaries
array_sy=substrate_width,
prepreg_t=prepreg_t,
l1_t=l1_t,
l2_t=l2_t,
l3_t=l3_t,
substrate_medium=RO4003C,
prepreg_medium=RO4450B,
metal_medium=patch_metal,
dl_hole=dl_hole,
dl_xy=dl_xy,
dl_z=dl_z,
)
mask = np.ones((array.Nx, array.Ny), dtype=bool)
mask[0, 0] = False
bool_array = xr.DataArray(
mask, # The value (can be False too)
dims=["x", "y"], # Names of the dimensions
)
all_structures, all_mesh_overrides, arrow_snapping_points = array.make_array(
bit_mask=bool_array, ground_width=substrate_width
)
via_center = unit_cell_1.calc_via_offset()
scene = td.Scene(structures=all_structures, plot_length_units="mm")
fig, axs = plt.subplots(1, 2, figsize=(10, 5), tight_layout=True)
scene.plot(ax=axs[0], z=top_l1, hlim=[-3 * mm, 3 * mm], vlim=[-3 * mm, 3 * mm])
scene.plot(ax=axs[1], z=bottom, hlim=[-3 * mm, 3 * mm], vlim=[-3 * mm, 3 * mm])
plt.show()
fig, axs = plt.subplots(1, 1, figsize=(10, 5), tight_layout=True)
scene.plot(ax=axs, x=via_center)
plt.show()
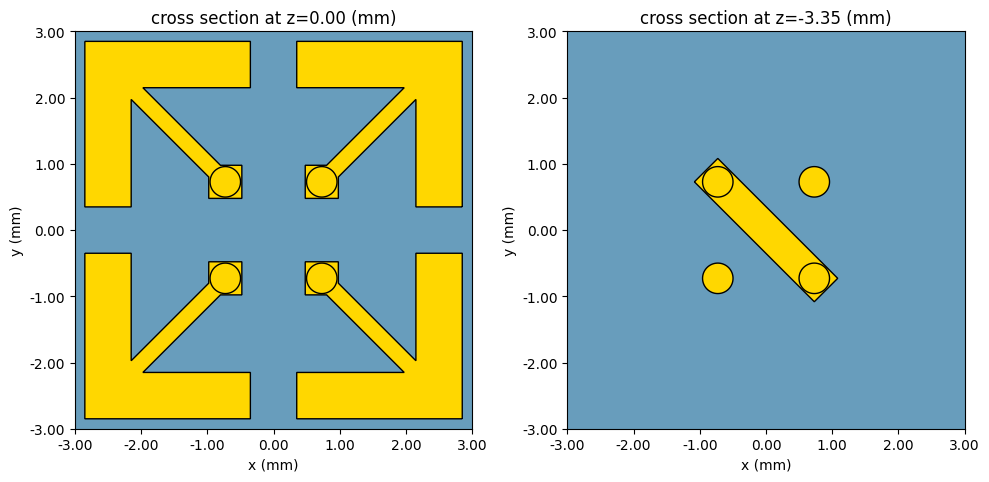
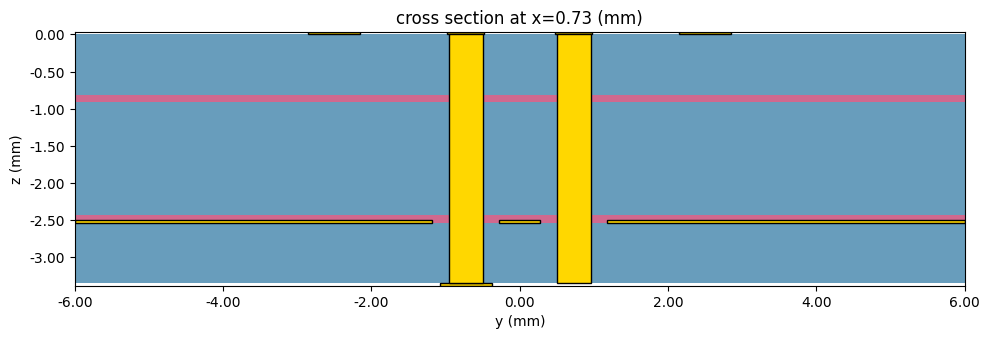
Simulation Setup#
Now we set up the electromagnetic simulation to characterize the PRUC. We use periodic boundary conditions in x and y to model an infinite array. A FieldMonitor is added just above the source to capture the reflected waves.
[6]:
boundary_spec = td.BoundarySpec(
x=td.Boundary.periodic(),
y=td.Boundary.periodic(),
z=td.Boundary.pml(),
)
time = td.GaussianPulse(freq0=freq0, fwidth=fwidth)
planewave = td.PlaneWave(
size=(td.inf, td.inf, 0),
center=(0, 0, 5 * mm),
source_time=time,
direction="-",
pol_angle=np.pi / 2,
num_freqs=1,
)
R_mon = td.FieldMonitor(
size=(td.inf, td.inf, 0), center=(0, 0, 15 * mm), name="reflection", freqs=freqs
)
sim = td.Simulation(
center=sim_center,
size=sim_size,
grid_spec=td.GridSpec.auto(
min_steps_per_wvl=10,
wavelength=td.C_0 / freq_stop,
override_structures=all_mesh_overrides,
snapping_points=arrow_snapping_points,
dl_min=0.018 * mm,
),
structures=all_structures,
sources=[planewave],
monitors=[R_mon],
run_time=run_time,
boundary_spec=boundary_spec,
)
print(f"Number of cells: {sim.grid.num_cells}")
print(
f"Smallest cell size (μm): ({np.min(sim.grid.sizes.x):.2f}, {np.min(sim.grid.sizes.y):.2f}, {np.min(sim.grid.sizes.z):.2f})"
)
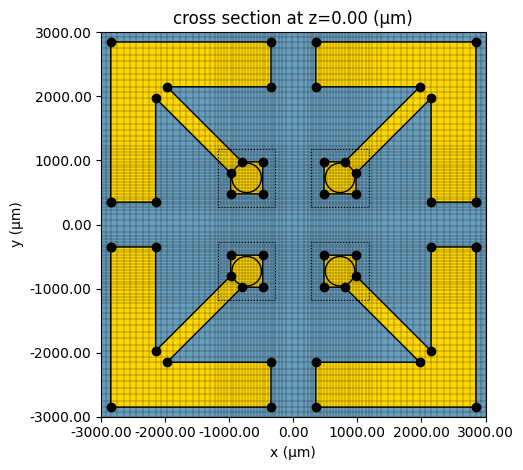
ax = sim.plot(z=top_l1)
ax = sim.plot_grid(ax=ax, z=top_l1)
plt.show()
10:15:24 CEST WARNING: ℹ️ ⚠️ RF simulations are subject to new license requirements in the future. You are using RF-specific components in this simulation. - Contains monitors defined for RF wavelengths.
Number of cells: [88, 88, 137]
Smallest cell size (μm): (35.66, 35.66, 33.50)
Bayesian Optimization Setup#
This section defines the key functions and parameters for optimizing the reflectarray unit cell design. To use the design plugin, we must provide a function that parameterizes the Simulation, as well as a function that calculates a metric which evaluates the fitness of the design.
In this notebook, we wish to optimize the fractional bandwidth of the unit cell by modifying the arrow stem length and the arrow head length of the PRUC. In the next section, we introduce a few helper functions with these tasks in mind.
Using these helper functions we setup a Bayesian optimization using the design plugin. The optimization is configured to run 50 initial iterations followed by 10 refinement iterations using an Upper Confidence Bound (UCB) acquisition function.
[7]:
def compute_flux_polarization_components(mon_data) -> tuple[float, float]:
"""Compute flux in the +z axis direction, but decomposed
into x and y electric field polarizations"""
Ex = mon_data.Ex
Ey = mon_data.Ey
Hx = mon_data.Hx
Hy = mon_data.Hy
Px = 0.5 * np.real(Ex * Hy.conj())
Py = 0.5 * np.real(-Ey * Hx.conj())
flux_x = Px.integrate(["x", "y"])
flux_y = Py.integrate(["x", "y"])
return flux_x, flux_y
def find_frequency_bounds(value_dB: xr.DataArray, threshold=-1) -> tuple[float, float]:
"""Find the frequency bounds where value_dB is above the threshold."""
value_dB = value_dB.squeeze()
peak_amp = value_dB.max().item()
peak_frequency = value_dB.idxmax(dim="f").item()
if peak_amp < threshold:
return np.nan, np.nan
below_threshold = (value_dB < threshold).values
low_freq = value_dB.f[below_threshold].where(value_dB.f < peak_frequency).max().item()
high_freq = value_dB.f[below_threshold].where(value_dB.f > peak_frequency).min().item()
return low_freq, high_freq
def calculate_fractional_bandwith_metric(mon_data: td.FieldData, threshold=-1) -> float:
"""Calculate the fractional bandwidth metric given a simulation result"""
flux_x, _ = compute_flux_polarization_components(mon_data)
# The co-polarization reflection coefficient in dB [1]. The source is normalized to 1 Watt.
Rxy_dB = 10 * np.log10(flux_x).squeeze()
peak = Rxy_dB.max().item()
if peak < threshold:
return 0.0
# Find the max value, and from there find where Rxy crosses the threshold of -1 dB.
low_freq, high_freq = find_frequency_bounds(Rxy_dB, threshold=threshold)
freq0 = (low_freq + high_freq) / 2
bandwidth = high_freq - low_freq
# Fractional bandwidth in percent
fractional_bandwidth = 100 * bandwidth / freq0
return fractional_bandwidth
def make_structures_and_gridspec(l_head: float, l_stem: float) -> tuple[td.Structure, td.GridSpec]:
"""Recreates the structures that are affected by a new arrow head length and stem length."""
# Update unit cell parameters
array.unit_cell_0.l_head = l_head
array.unit_cell_1.l_head = l_head
array.unit_cell_0.l_stem = l_stem
array.unit_cell_1.l_stem = l_stem
all_structures, all_mesh_overrides, arrow_snapping_points = array.make_array(
bit_mask=bool_array, ground_width=substrate_width
)
grid_spec = td.GridSpec.auto(
min_steps_per_wvl=10,
wavelength=td.C_0 / freq_stop,
override_structures=all_mesh_overrides,
snapping_points=arrow_snapping_points,
dl_min=0.018 * mm,
)
return all_structures, grid_spec
def pre(l_head, l_stem) -> td.Simulation:
"""Pre-processing function, which creates a ``Simulation`` from the design parameters."""
all_structures, grid_spec = make_structures_and_gridspec(l_head, l_stem)
return sim.updated_copy(structures=all_structures, grid_spec=grid_spec)
def post(data: td.SimulationData) -> float:
"""Post-processing function, which processes the tidy3d simulation data to return the function output."""
mon_data = data[R_mon.name]
frac_bw = calculate_fractional_bandwith_metric(mon_data, threshold=-1)
return frac_bw
# Setup of the parameters for the optimization step. The span indicates the bounds of the associated parameter.
param_l1 = tdd.ParameterFloat(name="l_head", span=(2.2 * mm, 2.83 * mm), num_points=1)
param_l2 = tdd.ParameterFloat(name="l_stem", span=(2.2 * mm, 3.4 * mm), num_points=2)
method = tdd.MethodBayOpt(
initial_iter=50,
n_iter=10,
acq_func="ucb",
kappa=0.6,
seed=1,
)
design_space = tdd.DesignSpace(parameters=[param_l1, param_l2], method=method)
Running the Optimization#
Next, we use the run command to start the optimization.
[8]:
results = design_space.run(pre, post, verbose=True)
10:15:26 CEST Running 50 Simulations
10:18:50 CEST Best Fit from Initial Solutions: 56.604
10:18:51 CEST Running 1 Simulations
10:19:01 CEST Running 1 Simulations
10:19:18 CEST Running 1 Simulations
10:19:48 CEST Running 1 Simulations
10:20:20 CEST Latest Best Fit on Iter 3: 58.209
10:20:21 CEST Running 1 Simulations
10:20:31 CEST Running 1 Simulations
10:21:03 CEST Running 1 Simulations
10:21:28 CEST Running 1 Simulations
10:21:38 CEST Running 1 Simulations
10:22:00 CEST Running 1 Simulations
10:22:09 CEST Best Result: 58.208955223880594 Best Parameters: l_head: 2596.2990867530775 l_stem: 2943.467020495493
The optimization results in a final design with a fractional bandwidth of 58%.
Post-Processing and Plotting#
The results from running the DesignSpace can be viewed as a pandas Dataframe for easy reference.
[9]:
result_df = results.to_dataframe()
print(result_df)
l_head l_stem output
0 2462.723863 3064.389392 16.885553
1 2200.072056 2562.799087 23.437500
2 2292.456211 2310.806314 10.131332
3 2317.343933 2614.672872 25.049702
4 2449.963509 2846.580081 35.876289
5 2464.092544 3022.263400 18.113208
6 2328.804917 3253.740924 11.978221
7 2217.254184 3004.561012 13.075061
8 2462.902025 2870.427794 37.344398
9 2288.443771 2437.721787 18.532819
10 2704.469078 3361.913891 28.471002
11 2397.457232 3030.787139 12.060302
12 2752.125166 3273.527996 25.891182
13 2253.577853 2246.865740 0.000000
14 2306.993164 3253.771004 11.978221
15 2261.958505 2705.329150 30.181087
16 2803.470404 2839.798342 22.978723
17 2635.882582 2578.618757 37.638376
18 2632.495584 3201.550806 33.730835
19 2211.521615 3100.173178 12.060302
20 2822.982486 3097.798785 28.832952
21 2376.679715 3147.135194 13.284133
22 2265.032384 2737.472231 29.149798
23 2772.415167 2552.336978 11.450382
24 2381.298463 2356.034287 14.800759
25 2212.201183 3014.602640 13.075061
26 2333.325713 2518.655991 22.396857
27 2509.691090 2264.035054 18.476499
28 2561.694091 2376.074290 30.260870
29 2571.262488 3039.710032 19.354839
30 2264.470690 2696.867185 27.766600
31 2637.472099 2697.015123 43.902439
32 2231.470679 2843.075687 34.426230
33 2618.190626 2817.866934 50.656660
34 2795.094696 2903.866049 32.119914
35 2769.143207 2364.969645 6.716418
36 2287.744099 3168.869546 12.110092
37 2450.536407 2398.425037 17.274472
38 2784.330406 2617.319032 12.815534
39 2673.011625 3071.197582 34.657040
40 2756.482837 2948.406648 42.323651
41 2673.093733 2618.678010 35.294118
42 2370.054572 3275.063462 11.978221
43 2469.697450 3357.808057 11.978221
44 2617.968144 2946.034864 56.603774
45 2272.289963 3339.387110 10.830325
46 2483.444644 2894.067537 37.344398
47 2457.126186 2484.432376 21.093750
48 2769.129098 2888.415384 36.325678
49 2201.808306 2940.573896 15.529412
50 2640.367296 2910.644674 52.671756
51 2608.103669 2930.054229 56.603774
52 2620.107926 2936.791251 55.787476
53 2596.299087 2943.467020 58.208955
54 2588.824524 2938.765801 42.323651
55 2603.690268 2950.648729 57.410882
56 2596.517303 2943.453058 58.208955
57 2594.052195 2951.397788 42.323651
58 2610.128107 2943.002309 56.603774
59 2610.116221 2950.940604 56.603774
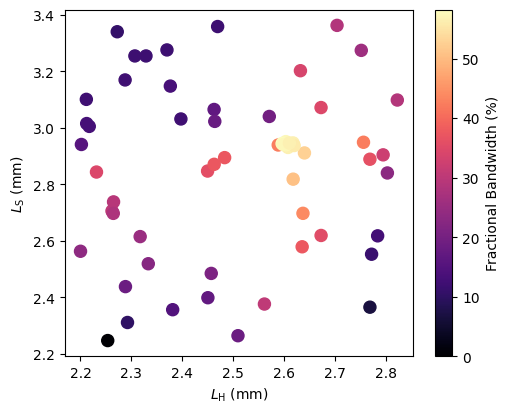
Another option is to make a scatter plot with the color scale indicating the fractional bandwidth. From the plot, it is evident that the highest fractional bandwidths are achieved where the stem length is around 2.9 mm and the head length is close to 2.6 mm.
[10]:
f, ax1 = plt.subplots(1, 1, figsize=(5, 4))
result_df_process = copy(result_df)
result_df_process["l_head"] = result_df_process["l_head"] * 1e-3
result_df_process["l_stem"] = result_df_process["l_stem"] * 1e-3
result_df_process = result_df_process.rename(columns={"output": "Fractional Bandwidth (%)"})
im = result_df_process.plot.scatter(
x="l_head", y="l_stem", s=75, c="Fractional Bandwidth (%)", cmap="magma", ax=ax1
)
ax1.set_xlabel(r"$L_{\rm H}$ (mm)")
ax1.set_ylabel(r"$L_{\rm S}$ (mm)")
plt.tight_layout(pad=0.2)
plt.show()
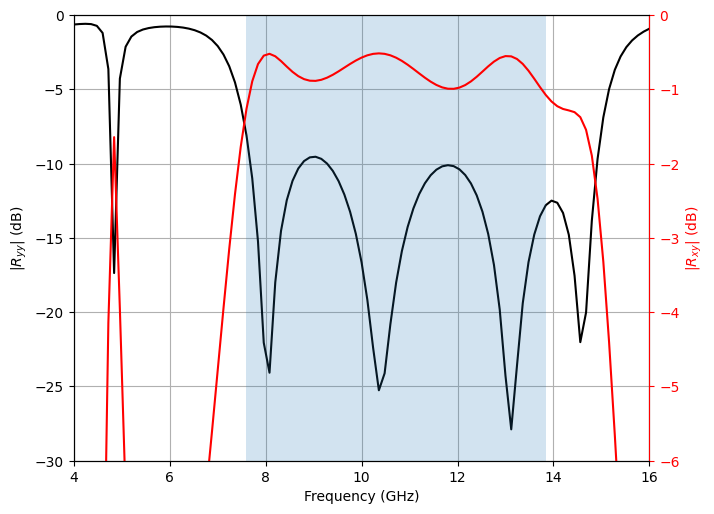
Finally, we plot the co- and cross-polarization reflection coefficients from the design with the maximum fractional bandwidth, over the frequencies from 4 GHz to 16 GHz.
[11]:
idx = result_df["output"].idxmax()
name = results.task_paths[idx]
sim_data = td.SimulationData.from_file(name)
flux_x, flux_y = compute_flux_polarization_components(sim_data[R_mon.name])
Rxy_dB = 10 * np.log10(flux_x.squeeze())
Ryy_dB = 10 * np.log10(flux_y.squeeze())
low_f, high_f = find_frequency_bounds(Rxy_dB)
bandwidth = high_f - low_f
fractional_bandwidth = calculate_fractional_bandwith_metric(sim_data[R_mon.name])
print(
f"Range {low_f * 1e-9:.2f}-{high_f * 1e-9:.2f} GHz, Bandwidth: {bandwidth * 1e-9:.2f} GHz, Fractional Bandwidth: {fractional_bandwidth:.2f}%"
)
fig, ax = plt.subplots(1, 1, figsize=(7, 5))
sub_ax = ax
ax2 = sub_ax.twinx()
(p1,) = sub_ax.plot(freqs / 1e9, Ryy_dB, "-k", label="Ryy-1")
(p2,) = ax2.plot(freqs / 1e9, Rxy_dB, "-r", label="Rxy-1")
ax2.axvspan(low_f / 1e9, high_f / 1e9, alpha=0.2)
sub_ax.set_xlabel("Frequency (GHz)")
sub_ax.set_ylabel(r"$|R_{yy}|$ (dB)")
sub_ax.set_xlim(4, 16)
sub_ax.set_xticks([4, 6, 8, 10, 12, 14, 16])
sub_ax.set_ylim(-30, 0)
sub_ax.grid(True)
ax2.set_ylabel(r"$|R_{xy}|$ (dB)")
ax2.set_ylim(-6, 0)
# Set axis colors
sub_ax.yaxis.label.set_color(p1.get_color())
ax2.yaxis.label.set_color(p2.get_color())
sub_ax.spines["right"].set_edgecolor(p1.get_color())
ax2.spines["right"].set_edgecolor(p2.get_color())
sub_ax.tick_params(axis="y", colors=p1.get_color())
ax2.tick_params(axis="y", colors=p2.get_color())
plt.tight_layout(pad=0.2)
plt.show()
Range 7.60-13.84 GHz, Bandwidth: 6.24 GHz, Fractional Bandwidth: 58.21%
References#
[1] H. Luyen, Z. Zhang, J. H. Booske, and N. Behdad, “Wideband, beam-steerable reflectarrays based on minimum-switch topology, polarization-rotating unit cells,” IEEE Access, vol. 7, pp. 36 568–36 578, 2019.