Adjoint analysis of a multi-layer slab#
In this notebook, we will show how to differentiate with respect to DiffractionMonitor outputs in tidy3d and also check the gradient values against gradients obtained using transfer matrix method (TMM), validating their accuracy for a multilayer slab problem.
[1]:
from typing import List, Tuple
import autograd as ag
import autograd.numpy as anp
import matplotlib.pyplot as plt
import numpy as np
import tidy3d as td
import tidy3d.web as web
import tmm
First, we define some global parameters describing the transmission through a multilayer slab with some spacing between each slab.
The layout is diagrammed below.
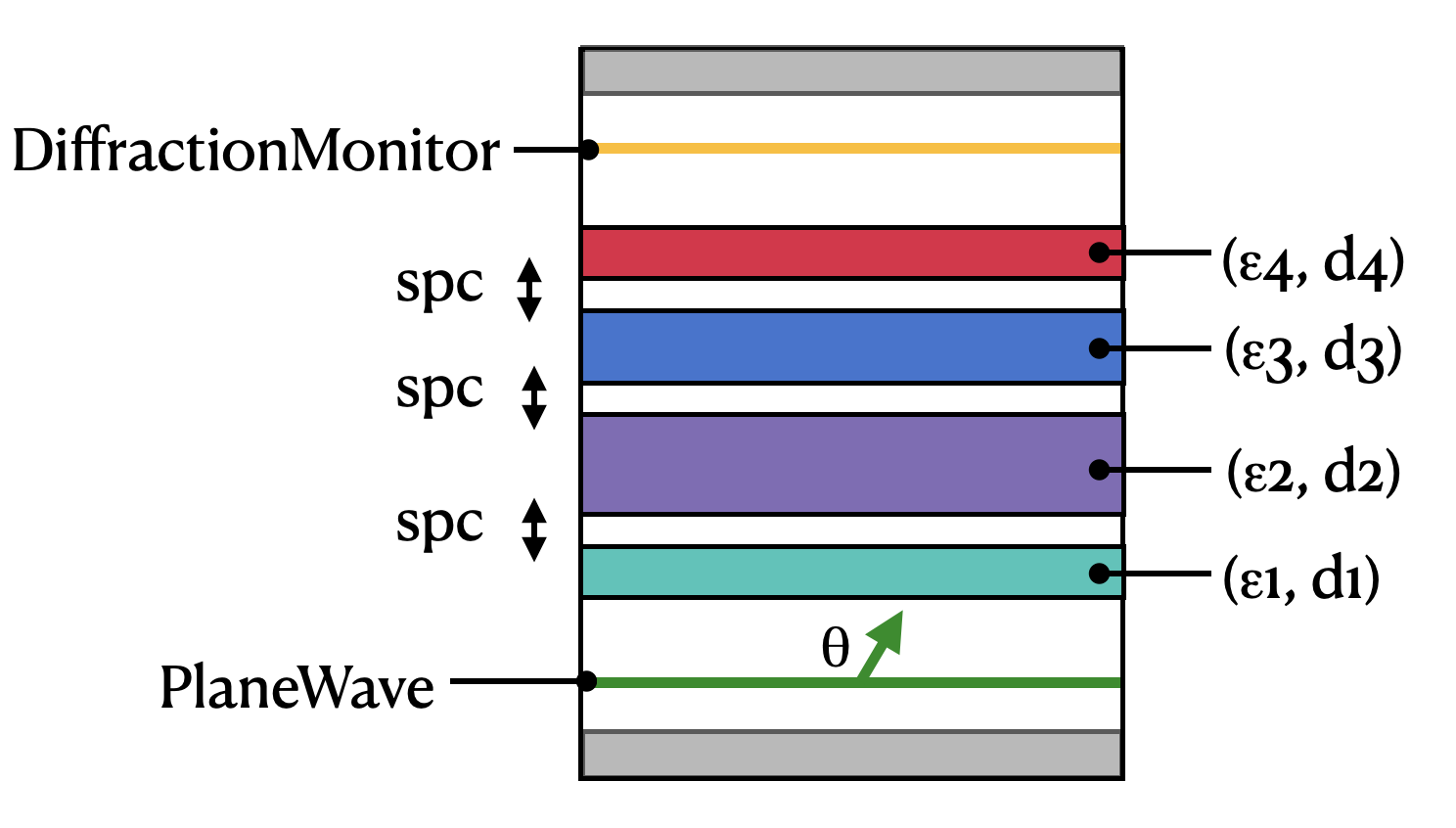
[2]:
# frequency we want to simulate at
freq0 = 2.0e14
k0 = 2 * np.pi * freq0 / td.C_0
freqs = [freq0]
wavelength = td.C_0 / freq0
# background permittivity
bck_eps = 1.0**2
# space between each slab
spc = 0.0
# slab permittivities and thicknesses
slab_eps0 = [2.0**2, 1.8**2, 1.5**2, 1.9**2]
slab_ds0 = [0.5, 0.25, 0.5, 0.5]
# incidence angle
theta = 0 * np.pi / 8
# resolution
dl = 0.01
Transfer Matrix Method (Ground Truth)#
Next we use the tmm package to write a function to return the transmission T of p polarized light given a set of slab permittivities and thicknesses. We’ll also write a function to compute the numerical gradient using TMM and will take these to be our “ground truths” when evaluating the accuracy of our values obtained through FDTD and autograd.
Transmission Calculation with TMM#
First, we write a function to compute transmission.
[3]:
def compute_T_tmm(slab_eps=slab_eps0, slab_ds=slab_ds0) -> float:
"""Get transmission as a function of slab permittivities and thicknesses."""
# construct lists of permittivities and thicknesses including spaces between
new_slab_eps = []
new_slab_ds = []
for eps, d in zip(slab_eps, slab_ds):
new_slab_eps.append(eps)
new_slab_eps.append(bck_eps)
new_slab_ds.append(d)
new_slab_ds.append(spc)
slab_eps = new_slab_eps[:-1]
slab_ds = new_slab_ds[:-1]
# add the input and output spaces to the lists
eps_list = [bck_eps] + slab_eps + [bck_eps]
n_list = np.sqrt(eps_list)
d_list = [np.inf] + slab_ds + [np.inf]
# compute transmission with TMM
return tmm.coh_tmm("p", n_list, d_list, theta, wavelength)["T"]
We run this function with our starting parameters and see that we get a transmission of about 98% for the set of input parameters.
[4]:
T_tmm = compute_T_tmm(slab_eps=slab_eps0, slab_ds=slab_ds0)
print(f"T (tmm) = {T_tmm:.3f}")
T (tmm) = 0.786
Numerical Gradient with TMM#
Next, we will use our compute_T_tmm() function to compute the “numerical” gradient to use as a comparison against our adjoint results with FDTD.
The derivative of a function \(f(x)\) w.r.t. \(x\) can be approximated using finite differences as
with a small step \(\Delta\).
To compute the gradient of our transmission with respect to each of the slab thicknesses and permittivities, we need to repeat this step for each of the values. Luckily, since TMM is very fast, we can compute these quantities quite quickly compared to if we were using FDTD.
Important note: We assume in our TMM numerical gradient that when the slabs are touching (
spc=0) and a slab thickness is modified, the thicknesses of the neighboring slabs adjust to accommodate this change. For example, if slabiincreases bydt, slabi-1andi+1each decrease bydt/2. We also account for this in our FDTD set up by keeping the centers of all boxes constant and not tracking the gradient through these quantities. The reason this is required is thattidy3ddoes not recognize the space between touchingtd.Boxobjects as a single interface and will instead “double count” the gradient contribution of the interface if they are placed right next to each other. One must therefore be careful about overlapping or touching twotd.Boxor other geometries when computing gradients.
Here we write the function to return the numerical gradient.
[5]:
def compute_grad_tmm(slab_eps=slab_eps0, slab_ds=slab_ds0) -> Tuple[List[float], List[float]]:
"""Compute numerical gradient of transmission w.r.t. each of the slab permittivities and thicknesses using TMM."""
delta = 1e-4
# set up containers to store gradient and perturbed arguments
num_slabs = len(slab_eps)
grad_tmm = np.zeros((2, num_slabs), dtype=float)
args = np.stack((slab_eps, slab_ds), axis=0)
# loop through slab index and argument index (eps, d)
for arg_index in range(2):
for slab_index in range(num_slabs):
grad = 0.0
# perturb the argument by delta in each + and - direction
for pm in (-1, +1):
args_num = args.copy()
args_num[arg_index][slab_index] += delta * pm
# NEW: for slab thickness gradient, need to modify neighboring slabs too
if arg_index == 1 and spc == 0:
if slab_index > 0:
args_num[arg_index][slab_index - 1] -= delta * pm / 2
if slab_index < num_slabs - 1:
args_num[arg_index][slab_index + 1] -= delta * pm / 2
# compute argument perturbed T and add to finite difference gradient contribution
T_tmm = compute_T_tmm(slab_eps=args_num[0], slab_ds=args_num[1])
grad += pm * T_tmm / 2 / delta
grad_tmm[arg_index][slab_index] = grad
grad_eps, grad_ds = grad_tmm
return grad_eps, grad_ds
Let’s run this function and observe the gradients. These will be saved later to compare against our autograd results.
[6]:
grad_eps_tmm, grad_ds_tmm = compute_grad_tmm()
print(f"gradient w.r.t. eps (tmm) = {grad_eps_tmm}")
print(f"gradient w.r.t. ds (tmm) = {grad_ds_tmm}")
gradient w.r.t. eps (tmm) = [-0.2766323 0.01377339 -0.2032054 -0.28999361]
gradient w.r.t. ds (tmm) = [-1.75199732 -0.21552416 1.00729645 -2.08209951]
FDTD#
Next, we will implement the same two functions using Tidy3D.
Transmission Calculation with FDTD#
We first write a function to compute the transmission of a multilayer slab using Tidy3D. We use a DiffractionMonitor to measure our transmission amplitudes. Below, we break up the transmission calculation into a few functions to make it easier to read and reuse later.
[7]:
from autograd.tracer import getval
def make_sim(slab_eps=slab_eps0, slab_ds=slab_ds0) -> td.Simulation:
"""Create a Simulation given the slab permittivities and thicknesses."""
# frequency setup
fwidth = freq0 / 10.0
freqs = [freq0]
# geometry setup
bck_medium = td.Medium(permittivity=bck_eps)
space_above = 2
space_below = 2
length_x = 1.0
length_y = 1.0
length_z = space_below + sum(slab_ds0) + space_above + (len(slab_ds0) - 1) * spc
sim_size = (length_x, length_y, length_z)
# make structures
slabs = []
z_start = -length_z / 2 + space_below
for d, eps in zip(slab_ds, slab_eps):
# don't track the gradient through the center of each slab
# as tidy3d doesn't have enough information to properly process the interface between touching Box objects
z_center = z_start + d / 2
z_center = getval(z_center)
slab = td.Structure(
geometry=td.Box(center=[0, 0, z_center], size=[td.inf, td.inf, d]),
medium=td.Medium(permittivity=eps),
)
slabs.append(slab)
z_start = z_start + d + spc
# source setup
gaussian = td.GaussianPulse(freq0=freq0, fwidth=fwidth)
src_z = -length_z / 2 + space_below / 2.0
source = td.PlaneWave(
center=(0, 0, src_z),
size=(td.inf, td.inf, 0),
source_time=gaussian,
direction="+",
angle_theta=theta,
angle_phi=0,
pol_angle=0,
)
# boundaries
boundary_x = td.Boundary.bloch_from_source(
source=source, domain_size=sim_size[0], axis=0, medium=bck_medium
)
boundary_y = td.Boundary.bloch_from_source(
source=source, domain_size=sim_size[1], axis=1, medium=bck_medium
)
boundary_spec = td.BoundarySpec(x=boundary_x, y=boundary_y, z=td.Boundary.pml(num_layers=40))
# monitors
mnt_z = length_z / 2 - space_above / 2.0
monitor_1 = td.DiffractionMonitor(
center=[0.0, 0.0, mnt_z],
size=[td.inf, td.inf, 0],
freqs=freqs,
name="diffraction",
normal_dir="+",
)
# make simulation
return td.Simulation(
size=sim_size,
# grid_spec=td.GridSpec.auto(min_steps_per_wvl=100),
grid_spec=td.GridSpec.uniform(dl=0.01),
structures=slabs,
sources=[source],
monitors=[monitor_1],
run_time=10 / fwidth,
boundary_spec=boundary_spec,
medium=bck_medium,
subpixel=True,
shutoff=1e-8,
)
Let’s generate a simulation and plot it to make sure it looks reasonable.
[8]:
sim = make_sim()
f, ax = plt.subplots(1, 1, figsize=(10, 10))
sim.plot(y=0, ax=ax)
plt.show()
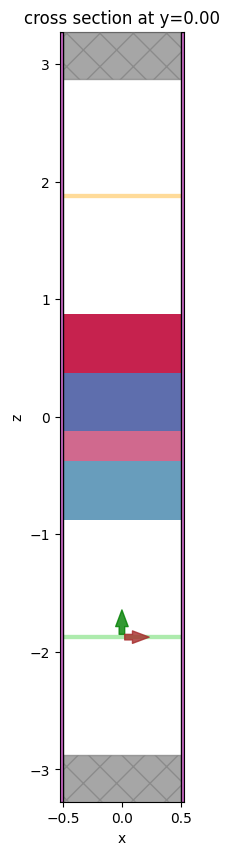
Now we write a function to post process some run results to get the transmission we are after.
[9]:
def post_process_T(sim_data: td.SimulationData) -> float:
"""Given some td.SimulationData from the run, return the transmission of "p" polarized light."""
amps = sim_data["diffraction"].amps.sel(polarization="p").values
return anp.sum(abs(amps) ** 2)
And finally, put everything together in a single function that relates the permittivities and thicknesses of each slab to the transmission, through a td.Simulation run.
[ ]:
def compute_T_fdtd(slab_eps=slab_eps0, slab_ds=slab_ds0) -> float:
"""Given the slab permittivities and thicknesses, compute T."""
sim = make_sim(slab_eps=slab_eps, slab_ds=slab_ds)
sim_data = web.run(sim, task_name="slab", verbose=True)
return post_process_T(sim_data)
[11]:
T_fdtd = compute_T_fdtd(slab_eps0, slab_ds0)
print(T_fdtd)
11:37:39 CEST Created task 'slab' with task_id 'fdve-2f3c27e3-3ee5-42e4-8393-61d87ca60df7' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId=fdve-2f3c27e3-3e e5-42e4-8393-61d87ca60df7'.
Task folder: 'default'.
11:37:41 CEST Maximum FlexCredit cost: 0.107. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
status = success
11:37:43 CEST loading simulation from simulation_data.hdf5
0.7851633658072134
Computing T and Gradient with FDTD#
Now that we have this function defined, we are ready to compute our transmission and gradients using Tidy3d.
We first call autograd.value_and_grad() on our transmission calculation function, which returns a function that will give us both T and the gradient of T with respect to the input parameters in one shot. For more details, see the previous tutorial.
[12]:
compute_T_and_grad_fdtd = ag.value_and_grad(compute_T_fdtd, argnum=(0, 1))
Next, we call this function on our starting parameters, which will kick off the original (fwd) T transmission simulation and then the reverse (adj) simulation, which is used in combination with fwd for the gradient calculation.
[13]:
T_fdtd, (grad_eps_fdtd, grad_ds_fdtd) = compute_T_and_grad_fdtd(slab_eps0, slab_ds0)
Created task 'slab' with task_id 'fdve-8c16e0d4-3e1b-4584-b58d-ec229fde8f38' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId=fdve-8c16e0d4-3e 1b-4584-b58d-ec229fde8f38'.
Task folder: 'default'.
11:37:45 CEST Maximum FlexCredit cost: 0.108. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
11:37:46 CEST status = success
11:37:49 CEST loading simulation from simulation_data.hdf5
11:37:51 CEST Started working on Batch containing 1 tasks.
11:37:52 CEST Maximum FlexCredit cost: 0.108 for the whole batch.
Use 'Batch.real_cost()' to get the billed FlexCredit cost after the Batch has completed.
11:38:14 CEST Batch complete.
Checking Accuracy of TMM (Numerical) vs FDTD (Adjoint)#
Let’s convert these from autograd types to numpy arrays to work with them easier, and then display the results compared to TMM.
[14]:
grad_eps_fdtd = np.array(grad_eps_fdtd)
grad_ds_fdtd = np.array(grad_ds_fdtd)
[15]:
print(f"T (tmm) = {T_tmm:.5f}")
print(f"T (FDTD) = {T_fdtd:.5f}")
T (tmm) = 0.78581
T (FDTD) = 0.78516
We see that the transmission results match very well with TMM, giving us a lot of confidence that our set up is correct.
Let’s look at the gradients now.
[16]:
print("un-normalized:")
print(f"\tgrad_eps (tmm) = {grad_eps_tmm}")
print(f"\tgrad_eps (FDTD) = {grad_eps_fdtd}")
print(80 * "-")
print(f"\tgrad_ds (tmm) = {grad_ds_tmm}")
print(f"\tgrad_ds (FDTD) = {grad_ds_fdtd}")
rms_eps = np.linalg.norm(grad_eps_tmm - grad_eps_fdtd) / np.linalg.norm(grad_eps_tmm)
rms_ds = np.linalg.norm(grad_ds_tmm - grad_ds_fdtd) / np.linalg.norm(grad_ds_tmm)
print(f"RMS error = {rms_eps * 100} %")
print(f"RMS error = {rms_ds * 100} %")
un-normalized:
grad_eps (tmm) = [-0.2766323 0.01377339 -0.2032054 -0.28999361]
grad_eps (FDTD) = [-0.2816894 0.01413387 -0.20661187 -0.29536459]
--------------------------------------------------------------------------------
grad_ds (tmm) = [-1.75199732 -0.21552416 1.00729645 -2.08209951]
grad_ds (FDTD) = [-1.78417308 -0.21968072 1.0273637 -2.12167783]
RMS error = 1.8092412469716965 %
RMS error = 1.8892656820829092 %
If we only care about the error in the “directions” of the gradients, we can compare their normalized versions to each other.
[17]:
def normalize(arr):
return arr / np.linalg.norm(arr)
grad_eps_tmm_norm = normalize(grad_eps_tmm)
grad_ds_tmm_norm = normalize(grad_ds_tmm)
grad_eps_fdtd_norm = normalize(grad_eps_fdtd)
grad_ds_fdtd_norm = normalize(grad_ds_fdtd)
rms_eps = np.linalg.norm(grad_eps_tmm_norm - grad_eps_fdtd_norm) / np.linalg.norm(grad_eps_tmm_norm)
rms_ds = np.linalg.norm(grad_ds_tmm_norm - grad_ds_fdtd_norm) / np.linalg.norm(grad_ds_tmm_norm)
[18]:
print("normalized:")
print(f"\tgrad_eps (tmm) = {grad_eps_tmm_norm}")
print(f"\tgrad_eps (FDTD) = {grad_eps_fdtd_norm}")
print(f"\tRMS error = {rms_eps * 100} %")
print(80 * "-")
print(f"\tgrad_ds (tmm) = {grad_ds_tmm_norm}")
print(f"\tgrad_ds (FDTD) = {grad_ds_fdtd_norm}")
print(f"\tRMS error = {rms_ds * 100} %")
normalized:
grad_eps (tmm) = [-0.61534061 0.03063751 -0.45200988 -0.64506151]
grad_eps (FDTD) = [-0.61546297 0.03088108 -0.45142613 -0.64534188]
RMS error = 0.07026238984429953 %
--------------------------------------------------------------------------------
grad_ds (tmm) = [-0.60214521 -0.07407365 0.34619844 -0.71559827]
grad_ds (FDTD) = [-0.6018371 -0.07410268 0.34655023 -0.71568417]
RMS error = 0.04763529583405276 %
In which case we see a very good agreement.