Visualizing geometries in Tidy3D#
This notebook provides a tutorial for plotting Tidy3D components before running them to get a sense of the geometry.
We also provide a comprehensive list of other tutorials such as how to define boundary conditions, how to defining spatially-varying sources and structures, how to model dispersive materials, and how to create FDTD animations.
[1]:
import matplotlib.pylab as plt
import numpy as np
import tidy3d as td
# set logging level to ERROR because we'll only create simulations for demonstration, we're not running them.
td.config.logging.level = "ERROR"
Simple, 2D plotting#
Geometries#
All Geometry objects, such as Box, Sphere, Cylinder, and
PolySlab, have a .plot() method that plots their geometries on a plane specified by coordinate=position syntax (eg. z=5.0).
[2]:
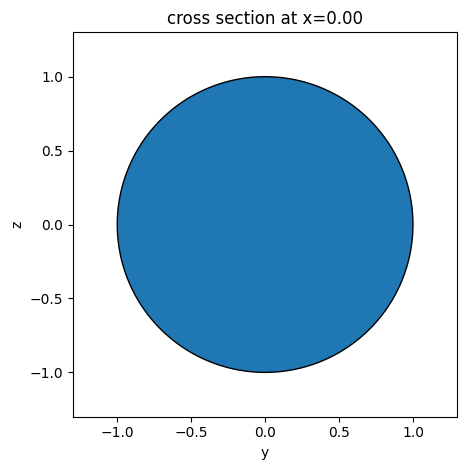
cylinder = td.Cylinder(center=(0, 0, 0), radius=1, length=2, axis=0)
ax = cylinder.plot(x=0)
plt.show()
Structures#
Structure objects, which combine a Geometry with a Medium, work the same way.
[3]:
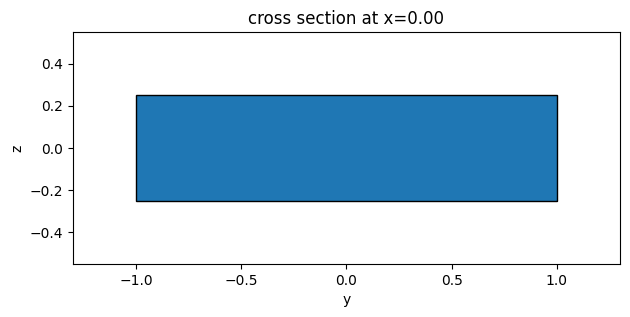
box = td.Structure(
geometry=td.Box(center=(0.0, 0.0, 0), size=(4, 2.0, 0.5)),
medium=td.Medium(permittivity=2.0),
)
ax = box.plot(x=0)
We can supply ax argument to the plot function to plot on a specific Matplotlib Axes, for example
[4]:
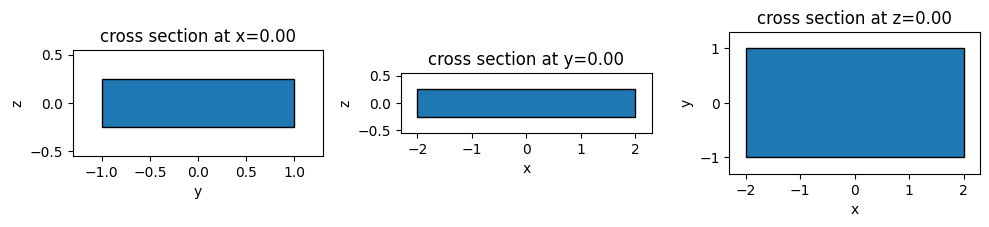
# make 3 columns of axes
f, (ax1, ax2, ax3) = plt.subplots(1, 3, tight_layout=True, figsize=(10, 3))
# plot each axis of the plot on each subplot
ax1 = box.plot(x=0, ax=ax1)
ax2 = box.plot(y=0, ax=ax2)
ax3 = box.plot(z=0, ax=ax3)
The .plot() method returns either a new axis (if ax not supplied) or the original axis, so you can add more objects to the plot, or edit it through the ax handle.
[5]:
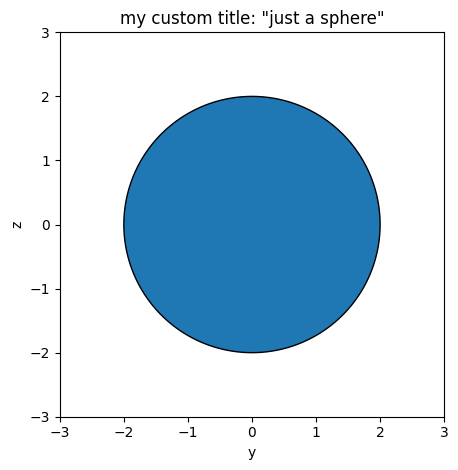
sphere = td.Structure(
geometry=td.Sphere(center=(0, 0, 0), radius=2), medium=td.Medium(permittivity=3)
)
ax = sphere.plot(x=0)
ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)
ax.set_title('my custom title: "just a sphere"')
plt.show()
Finally, since the geometry plotting us done using matplotlib Patches, you can supply optional keyword arguments to .plot() to change the display of the plot.
See matplotlib’s documentation on Patches for more information on arguments are accepted.
[6]:
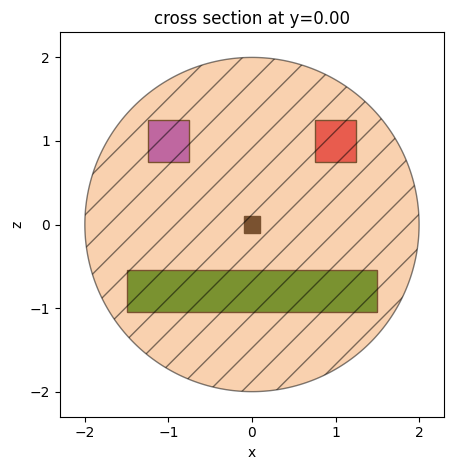
box1 = td.Box(center=(1.0, 0.0, 1), size=(0.5, 0.5, 0.5))
box2 = td.Box(center=(-1.0, 0.0, 1), size=(0.5, 0.5, 0.5))
box3 = td.Box(center=(0, 0.0, 0.0), size=(0.2, 0.2, 0.2))
box4 = td.Box(center=(0.0, 0.0, -0.8), size=(3, 0.5, 0.5))
ax = box1.plot(y=0, facecolor="crimson", edgecolor="black", alpha=1)
ax = box2.plot(y=0, ax=ax, facecolor="blueviolet", edgecolor="black", alpha=1)
ax = box3.plot(y=0, ax=ax, facecolor="black", edgecolor="black", alpha=1)
ax = box4.plot(y=0, ax=ax, facecolor="green", edgecolor="black", alpha=1)
ax = sphere.plot(y=0, ax=ax, facecolor="sandybrown", edgecolor="black", alpha=0.5, hatch="/")
Simulations#
We can plot all components contained in Simulation with the Simulation.plot() method.
Let’s create a simulation with a source, monitor, and a bunch of randomly placed spheres made of 3 distinct Medium objects.
[7]:
from numpy.random import random
L = 5 # length of simulation on all sides
def rand():
return L * (random() - 0.5)
# make random list of structures
structures = [
td.Structure(
geometry=td.Sphere(center=(rand(), rand(), rand()), radius=1),
medium=td.Medium(permittivity=np.random.choice([2.0, 2.5, 3.0, 3.5, 4.0])),
)
for i in range(20)
]
source = td.UniformCurrentSource(
center=(0, 0, -L / 3),
size=(L, L / 2, 0),
polarization="Ex",
source_time=td.GaussianPulse(
freq0=100e14,
fwidth=10e14,
),
)
monitor = td.FieldMonitor(center=(-L / 4, 0, 0), size=(L / 2, L, 0), freqs=[100e14], name="fields")
# make simulation from structures
sim = td.Simulation(
size=(L, L, L),
grid_spec=td.GridSpec.auto(wavelength=4),
boundary_spec=td.BoundarySpec(
x=td.Boundary.pml(num_layers=10),
y=td.Boundary.periodic(),
z=td.Boundary.pml(num_layers=10),
),
structures=structures,
sources=[source],
monitors=[monitor],
run_time=1e-12,
)
[8]:
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 10))
ax1 = sim.plot(x=0, ax=ax1)
# put the grid lines on the 2nd one
ax2 = sim.plot(x=0, ax=ax2)
ax2 = sim.plot_grid(x=0, ax=ax2)
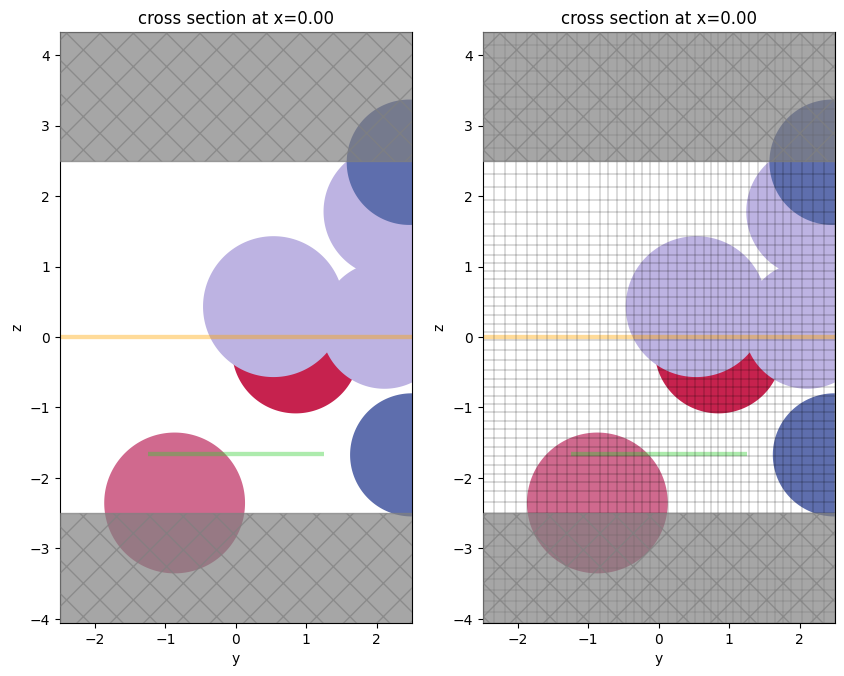
As of 2.4, Simulation.plot() and Simulation.plot_eps() have bounding plot options. One can implement a horizontal range of plotting (hlim) and/or a vertical range of plotting (vlim):
[9]:
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 10))
ax1 = sim.plot(x=0, ax=ax1, vlim=[-2, 2])
# put the grid lines on the 2nd one
ax2 = sim.plot(x=0, ax=ax2, hlim=[-1, 1], vlim=[-2, 2])
ax2 = sim.plot_grid(x=0, ax=ax2, hlim=[-1, 1], vlim=[-2, 2])
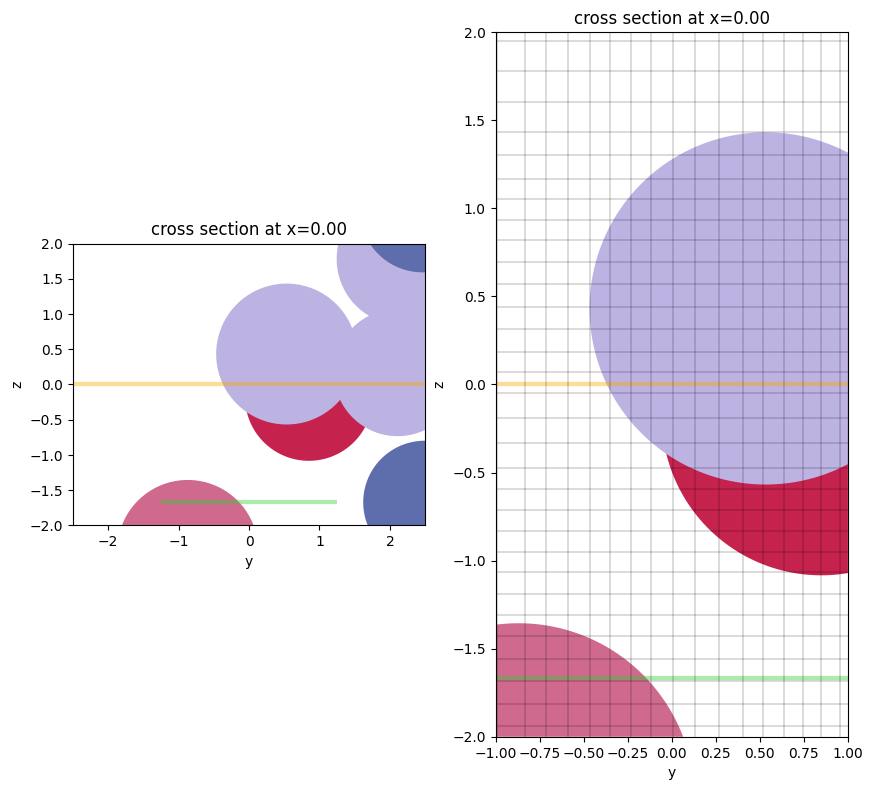
Plotting Materials#
with sim.plot we can plot each distinct material, source, monitor, and PML.
Note, all structures with same Medium show up as the same color.
[10]:
f, axes = plt.subplots(1, 3, tight_layout=True, figsize=(10, 3))
for ax, axis in zip(axes, "xyz"):
ax = sim.plot(**{axis: 0}, ax=ax)
ax.set_title(f"axis={axis}, position=0.0")
plt.show()
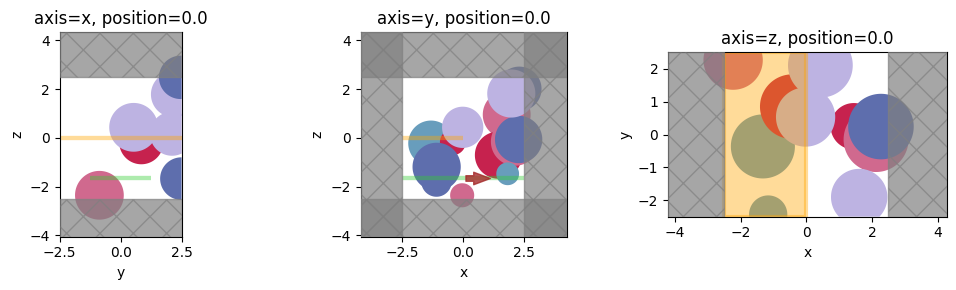
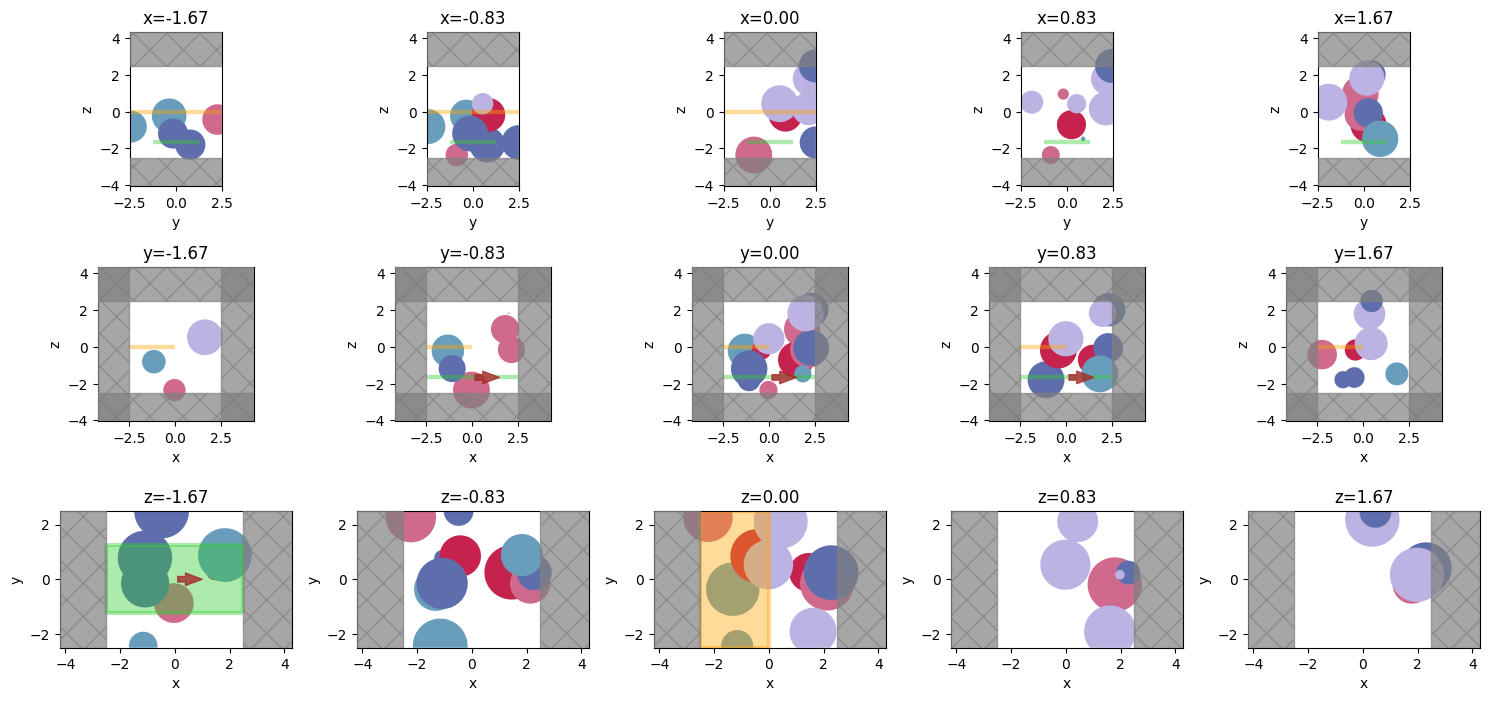
We can even get fancy and plot the cross sections at different positions along the 3 axes.
[11]:
npos = 5
positions = np.linspace(-L / 3, L / 3, npos)
f, axes = plt.subplots(3, npos, tight_layout=True, figsize=(npos * 3, 7))
for axes_range, axis in zip(axes, "xyz"):
for ax, pos in zip(axes_range, positions):
ax = sim.plot(**{axis: pos}, ax=ax)
ax.set_title(f"{axis}={pos:.2f}")
plt.show()
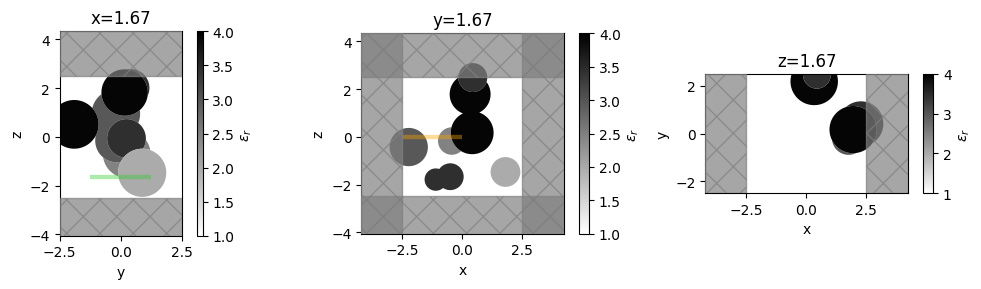
Plotting Permittivity#
With Simulation.plot_eps we can plot the continuously varying permittivity distribution on the plane.
[12]:
f, axes = plt.subplots(1, 3, tight_layout=True, figsize=(10, 3))
for ax, axis in zip(axes, "xyz"):
ax = sim.plot_eps(**{axis: pos}, ax=ax, alpha=0.98)
ax.set_title(f"{axis}={pos:.2f}")
plt.show()
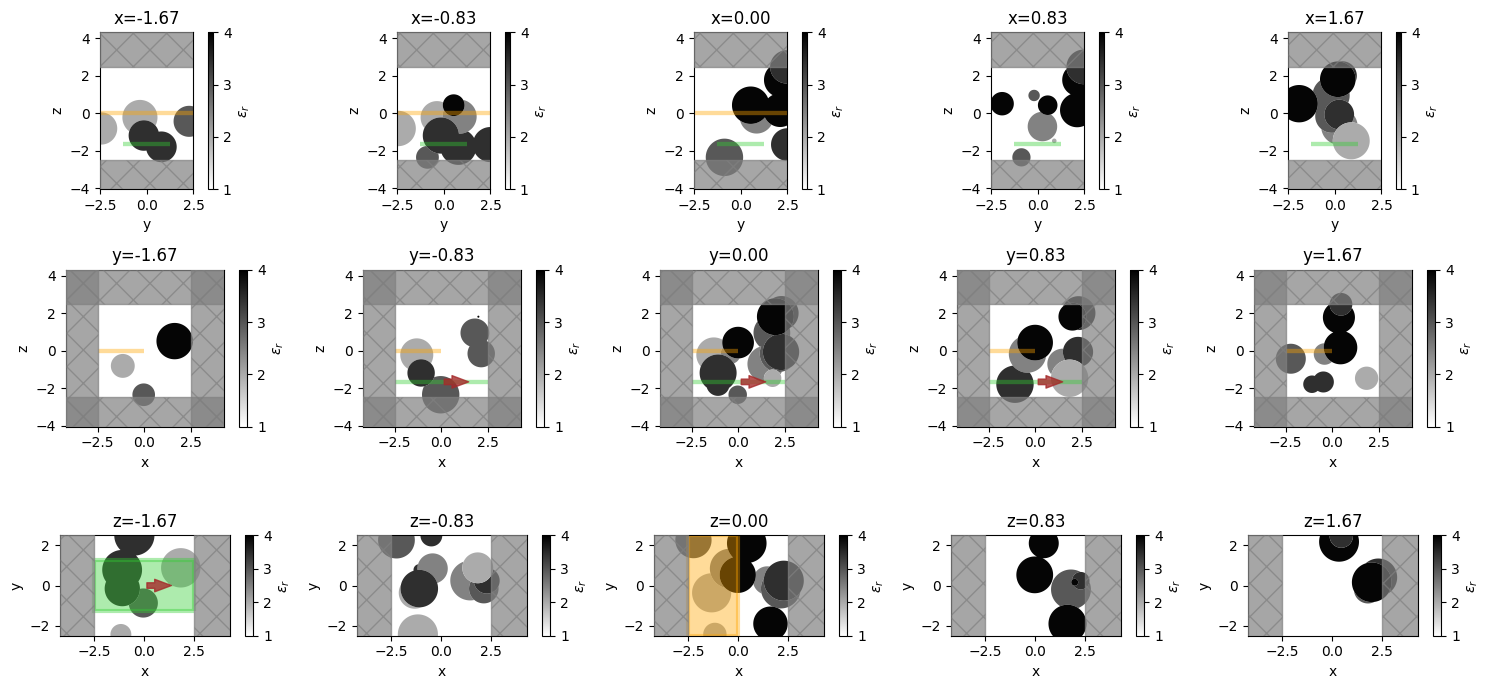
[13]:
npos = 5
positions = np.linspace(-L / 3, L / 3, npos)
f, axes = plt.subplots(3, npos, tight_layout=True, figsize=(npos * 3, 7))
for axes_range, axis in zip(axes, "xyz"):
for ax, pos in zip(axes_range, positions):
ax = sim.plot_eps(**{axis: pos}, ax=ax, alpha=0.98)
ax.set_title(f"{axis}={pos:.2f}")
plt.show()
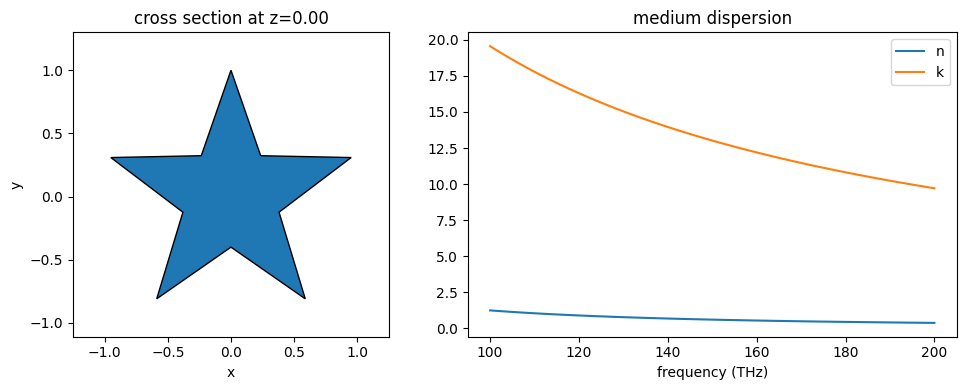
Plotting Other Quantities#
Structure + Medium#
The Structure.medium refractive index values over frequency can be plotted with it’s .plot() method as well.
[14]:
# import silver from material library
from tidy3d import material_library
Ag = material_library["Ag"]["Rakic1998BB"]
# make a star-shaped PolySlab
import numpy as np
r_in = 0.4
r_out = 1.0
inner_vertices = [
(
r_in * np.cos(2 * np.pi * i / 5 + np.pi / 2 - np.pi / 5),
r_in * np.sin(2 * np.pi * i / 5 + np.pi / 2 - np.pi / 5),
)
for i in range(5)
]
outer_vertices = [
(
r_out * np.cos(2 * np.pi * i / 5 + np.pi / 2),
r_out * np.sin(2 * np.pi * i / 5 + np.pi / 2),
)
for i in range(5)
]
star_vertices = []
for i in range(5):
star_vertices.append(inner_vertices[i])
star_vertices.append(outer_vertices[i])
poly_star = td.PolySlab(vertices=star_vertices, slab_bounds=(-1, 1), axis=2)
# make a star structure with silver as medium
silver_star = td.Structure(geometry=poly_star, medium=Ag)
# plot the structure alongside the medium properties
freqs = np.linspace(1e14, 2e14, 101)
position = 0.0
axis = 2
f, (ax1, ax2) = plt.subplots(1, 2, tight_layout=True, figsize=(10, 4))
ax1 = silver_star.geometry.plot(z=0, edgecolor="black", ax=ax1)
ax2 = silver_star.medium.plot(freqs=freqs, ax=ax2)
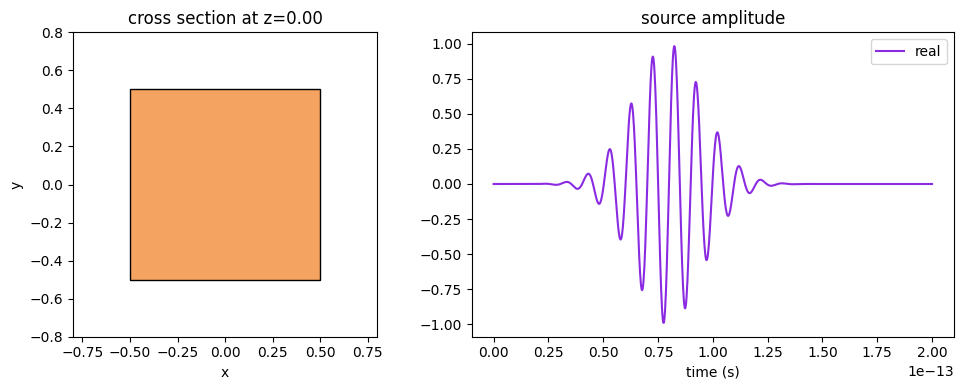
Source + Source Time#
Similarly, the Source.source_time amplitude over time can be plotted with its .plot() method.
[15]:
cube_source = td.UniformCurrentSource(
center=(0, 0, 0),
size=(1, 1, 1),
polarization="Ex",
source_time=td.GaussianPulse(
freq0=1e14,
fwidth=1e13,
),
)
times = np.linspace(0, 0.2e-12, 1001)
position = 0.0
axis = 2
f, (ax1, ax2) = plt.subplots(1, 2, tight_layout=True, figsize=(10, 4))
ax1 = cube_source.geometry.plot(z=0, facecolor="sandybrown", edgecolor="black", ax=ax1)
ax2 = cube_source.source_time.plot(times=times, ax=ax2)
Monitor#
[16]:
freq_mon = td.FieldMonitor(
center=(0, 0, 0),
size=(1, 1, 1),
freqs=list(np.linspace(1e14, 2e14, 11)),
name="test",
)
position = 0.0
axis = 2
ax = freq_mon.geometry.plot(z=0, facecolor="blueviolet", edgecolor="black")
[17]:
time_mon = td.FieldTimeMonitor(
center=(0, 0, 0),
size=(1, 1, 1),
interval=10,
name="test",
)
position = 0.0
axis = 2
ax = time_mon.geometry.plot(z=0, facecolor="blueviolet", edgecolor="black")
3D Plotting#
Tidy3D now supports interactive 3D plotting of simulations through jupyter notebooks.
To render, call simulation.plot_3d()
[18]:
sim.plot_3d()
[ ]: