Dynamic Derivatives Using Sliding Interfaces#
This notebook demonstrates how to obtain dynamic stability derivatives by simulating unsteady flow over a NACA0012 wing that pitches back and forth within a sliding interface.
Geometry#
The wing geometry has:
Chord \(c\) = 1 m
Span \(b\) = 2 m
Reference area \(A_{ref}\) = 2 m²
Moment length = [\(b\)/2, \(c\), \(b\)/2] = [1, 1, 1] m
Moment center = [0, 0, 0] (at quarter-chord, midspan)
Simulation Strategy#
Steady Initialization:
Ramp CFL from 1 to 100 over 1000 steps for robust convergence
Fixed sliding interface (zero angular velocity) to establish baseline flow
Maximum 10000 steps to ensure convergence
Unsteady Oscillation:
Sliding interface updated to oscillating motion
Sinusoidal pitching with amplitude 2° and frequency 2.5 flowthru/rad
400 time steps (4 complete cycles)
1. Download tutorial files#
[1]:
import math
import flow360 as fl
from flow360.examples import TutorialDynamicDerivatives
TutorialDynamicDerivatives.get_files()
The downloaded files include the geometry (CSM format) for the NACA0012 wing.
2. Create project from geometry#
[2]:
project = fl.Project.from_geometry(
TutorialDynamicDerivatives.geometry,
name="Tutorial Calculating Dynamic Derivatives using Sliding Interfaces from Python",
)
geometry = project.geometry
geometry.group_faces_by_tag("faceName")
[09:57:06] INFO: Geometry successfully submitted: type = Geometry name = Tutorial Calculating Dynamic Derivatives using Sliding Interfaces from Python id = geo-e863d8e0-f3b6-4dd9-ba79-ff8cb38d3272 status = uploaded project id = prj-9f2dbc33-dc46-4fa8-a385-82b4f61cc317
INFO: Waiting for geometry to be processed.
The wing is enclosed in a cylindrical sliding interface as shown below:
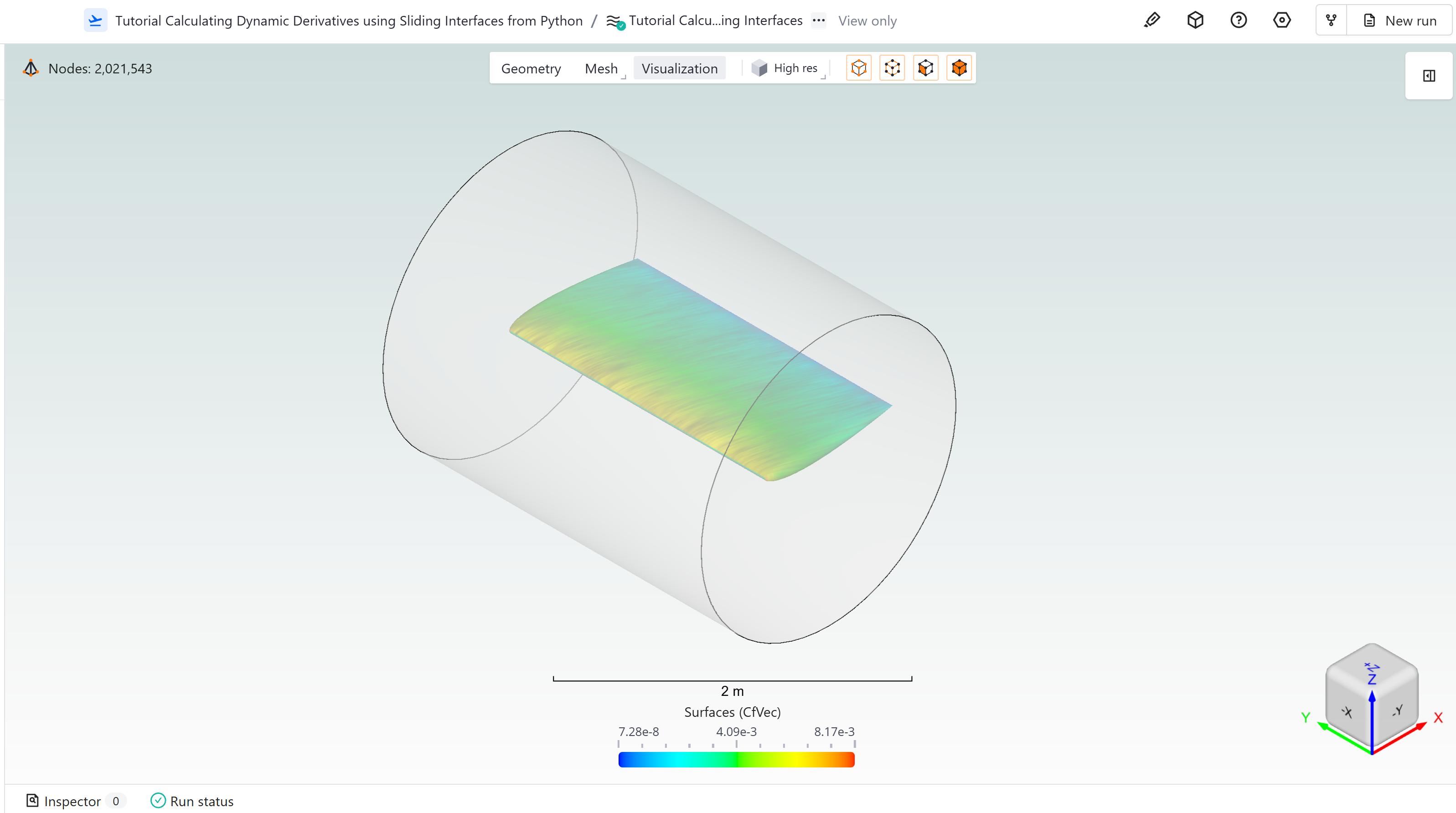
Figure: Wing enclosed in cylindrical sliding interface. The interface rotates about the y-axis, causing the wing to pitch.
3. Define sliding interface and meshing parameters#
The wing is enclosed in a cylindrical sliding interface:
Radius = 1.0 m
Height = 2.5 m
Rotation center = [0, 0, 0]
Rotation axis = y-axis [0, 1, 0]
[3]:
with fl.SI_unit_system:
cylinder = fl.Cylinder(
name="cylinder",
axis=[0, 1, 0],
center=[0, 0, 0],
inner_radius=0,
outer_radius=1.0,
height=2.5,
)
sliding_interface = fl.RotationVolume(
spacing_axial=0.04,
spacing_radial=0.04,
spacing_circumferential=0.04,
entities=cylinder,
enclosed_entities=geometry["wing"],
)
farfield = fl.AutomatedFarfield(name="farfield")
[09:57:33] INFO: using: SI unit system for unit inference.
Key meshing parameters:
Automated meshing with sliding interface and farfield zones
Refined leading and trailing edges for accuracy
Boundary layer resolved with first layer thickness of 1e-6 m
[4]:
with fl.SI_unit_system:
meshing_params = fl.MeshingParams(
defaults=fl.MeshingDefaults(
surface_max_edge_length=0.03 * fl.u.m,
curvature_resolution_angle=8 * fl.u.deg,
surface_edge_growth_rate=1.15,
boundary_layer_first_layer_thickness=1e-6,
boundary_layer_growth_rate=1.15,
),
refinement_factor=1.0,
volume_zones=[sliding_interface, farfield],
refinements=[
fl.SurfaceEdgeRefinement(
name="leadingEdge",
method=fl.AngleBasedRefinement(value=1 * fl.u.degree),
edges=geometry["leadingEdge"],
),
fl.SurfaceEdgeRefinement(
name="trailingEdge",
method=fl.HeightBasedRefinement(value=0.001),
edges=geometry["trailingEdge"],
),
],
)
INFO: using: SI unit system for unit inference.
4. Run steady case to initialize the flow field#
First, we run a steady case with a fixed sliding interface (zero angular velocity) to initialize the flow field. This provides a converged solution to start the unsteady simulation.
[5]:
with fl.SI_unit_system:
params = fl.SimulationParams(
meshing=meshing_params,
reference_geometry=fl.ReferenceGeometry(
moment_center=[0, 0, 0],
moment_length=[1, 1, 1],
area=2,
),
operating_condition=fl.AerospaceCondition(
velocity_magnitude=50,
),
time_stepping=fl.Steady(
max_steps=10000,
CFL=fl.RampCFL(initial=1, final=100, ramp_steps=1000),
),
outputs=[
fl.VolumeOutput(name="VolumeOutput", output_fields=["Mach"]),
fl.SurfaceOutput(
name="SurfaceOutput",
surfaces=geometry["*"],
output_fields=["Cp", "CfVec"],
),
],
models=[
fl.Rotation(
volumes=cylinder,
spec=fl.AngularVelocity(0 * fl.u.rad / fl.u.s),
),
fl.Freestream(surfaces=farfield.farfield, name="Freestream"),
fl.Wall(surfaces=geometry["wing"], name="NoSlipWall"),
fl.Fluid(
navier_stokes_solver=fl.NavierStokesSolver(
absolute_tolerance=1e-9,
linear_solver=fl.LinearSolver(max_iterations=35),
),
turbulence_model_solver=fl.SpalartAllmaras(
absolute_tolerance=1e-8,
linear_solver=fl.LinearSolver(max_iterations=25),
),
),
],
)
project.run_case(
params=params, name="Tutorial Dynamic Derivatives - Steady Initialization"
)
steady_case = fl.Case.from_cloud(project.case.id)
INFO: using: SI unit system for unit inference.
INFO: using: SI unit system for unit inference.
[09:57:36] INFO: Successfully submitted: type = Case name = Tutorial Dynamic Derivatives - Steady Initialization id = case-fc35883b-74e5-4ac9-9697-17e0a3e6a1bc status = pending project id = prj-9f2dbc33-dc46-4fa8-a385-82b4f61cc317
5. Understanding the Oscillation Setup#
The sliding interface oscillates according to the angle expression:
Where:
\(A\) = 0.0349066 rad (equivalent to 2°) - amplitude of oscillation
\(\omega_\text{non-dim}\) = nondimensional angular frequency
\(t_\text{non-dim}\) = nondimensional time
Calculating the nondimensional frequency:
We want the wing to complete one oscillation cycle over a specific number of flowthroughs. In this example, we use \(n\) = 2.5 flowthru/rad, meaning when \(\omega \cdot t\) changes by 1 radian, the air flows through 2.5 chord lengths.
Given:
Freestream velocity \(U_\infty\) = 50 m/s
Chord \(c\) = 1 m
Speed of sound \(C_\infty\) = 340.294 m/s
Grid unit \(L_\text{gridUnit}\) = 1 m
Physical angular frequency:
Nondimensional angular frequency:
Time step size:
We split each oscillation period into 100 steps:
6. Run unsteady case with oscillating interface#
Now we update the simulation parameters for the unsteady case and fork from the steady solution. Only the time stepping and rotation spec need to be modified.
[6]:
# Update parameters for unsteady case
with fl.SI_unit_system:
params.time_stepping = fl.Unsteady(
max_pseudo_steps=80,
steps=400,
step_size=0.01 * 2.0 * math.pi / 20.0 * fl.u.s,
CFL=fl.RampCFL(initial=1, final=1e8, ramp_steps=20),
)
params.models[0].spec = fl.AngleExpression("0.0349066 * sin(0.05877271 * t)")
# Run unsteady case forked from steady solution
project.run_case(
params=params,
name="Tutorial Dynamic Derivatives - Unsteady Oscillation",
fork_from=steady_case,
)
unsteady_case = project.case
INFO: using: SI unit system for unit inference.
INFO: using: SI unit system for unit inference.
[09:57:37] INFO: using: SI unit system for unit inference.
[09:57:38] INFO: Successfully submitted: type = Case name = Tutorial Dynamic Derivatives - Unsteady Oscillation id = case-e040a828-b521-432a-8402-5e1c58dcb612 status = pending project id = prj-9f2dbc33-dc46-4fa8-a385-82b4f61cc317
7. Postprocessing - Extract Dynamic Derivatives#
Once the simulation is complete, we download the results and calculate the dynamic derivatives. The key output is the total_forces data which contains force and moment coefficients at each time step.
[7]:
import flow360 as fl
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
cmap = plt.colormaps["tab10"]
# Load completed example case from the example library (flow360 25.8 or above)
project = fl.Project.from_example(by_name="Dynamic Derivatives")
case = project.get_case()
# Note that in this example we're loading a pre-computed unsteady case from the example library,
# so the reader doesn't need to wait for the simulation to finish.
# For production usage, the user can use:
# case = unsteady_case
# or:
# case = fl.Case.from_cloud("your-case-id")
# Download and load results
case.results.total_forces.download(to_file="total_forces.csv")
case.results.total_forces.load_from_local("total_forces.csv")
total_forces = case.results.total_forces.as_dataframe()
INFO: Found closest match for 'Dynamic Derivatives': 'Calculating Dynamic Derivatives using Sliding Interfaces' (similarity: 50.67 %)
[09:57:39] INFO: Copy operation started for project prj-0ad2a0d2-873f-43cc-b38a-a4e4e7b7268c. Waiting for completion...
[09:57:51] INFO: Copy operation completed successfully.
[09:57:53] INFO: Saved to total_forces.csv
Extract unique physical steps#
The total_forces data contains multiple rows per physical step (one per pseudo-step). We extract the final converged value at each physical step.
[8]:
def extract_unique_physical_steps(input_df):
"""Extract the row at the last pseudo step at the end of each physical step."""
physical_steps_raw = input_df["physical_step"]
n_rows = len(physical_steps_raw)
selected_row_index = []
for i in range(n_rows - 1):
if physical_steps_raw.iloc[i + 1] > physical_steps_raw.iloc[i]:
selected_row_index.append(i)
selected_row_index.append(n_rows - 1)
output = pd.DataFrame()
for k, v in input_df.items():
output[k] = [v.iloc[j] for j in selected_row_index]
return output.reset_index(drop=True)
total_forces = extract_unique_physical_steps(total_forces)
print(f"Number of physical steps: {len(total_forces)}")
Number of physical steps: 400
Calculate nondimensional time, angle of attack, and pitch rate#
We compute:
Nondimensional time from physical steps
Angle of attack \(\alpha = A \sin(\omega t)\)
Pitch rate \(\dot{\alpha}\) using central differences, converted to rad/flowthru
[9]:
# Define simulation parameters
length_unit = case.params.private_attribute_asset_cache.project_length_unit # m
U_inf = case.params.operating_condition.velocity_magnitude # m/s
C_inf = 340.29400580821283 * fl.u.m / fl.u.s # speed of sound
n_chord_per_period = 2.5 # flowthru/rad
chord = 1 * fl.u.m
omega_physical = U_inf / (n_chord_per_period * chord) # 1/s
omega_nondim = omega_physical / (C_inf / length_unit)
time_step_size_nondim = 0.01 * 2 * np.pi / omega_nondim # nondim
amplitude_deg = 2 * fl.u.deg
amplitude_rad = amplitude_deg.to(fl.u.rad)
def compute_time_nondim(df):
"""Compute nondimensional time from physical step."""
n_steps = len(df["physical_step"])
df["time_nondim"] = np.zeros(n_steps)
for i in range(n_steps):
df.loc[i, "time_nondim"] = time_step_size_nondim * (
df.loc[i, "physical_step"] + 1
)
def compute_alpha_dot(df):
"""Compute angle of attack and pitch rate."""
n_steps = len(df["physical_step"])
df["alpha"] = np.zeros(n_steps)
df["alpha_dot"] = np.zeros(n_steps)
alpha_eq_0_index = []
# Compute alpha
for i in range(n_steps):
t = df.loc[i, "time_nondim"]
df.loc[i, "alpha"] = amplitude_rad * np.sin(omega_nondim * t)
# Compute alpha_dot using central difference
for i in range(1, n_steps - 1):
df.loc[i, "alpha_dot"] = (
(df.loc[i + 1, "alpha"] - df.loc[i - 1, "alpha"])
/ (2 * time_step_size_nondim)
* C_inf
/ length_unit
* chord
/ U_inf
)
if abs(df.loc[i, "alpha"]) < 1e-10:
alpha_eq_0_index.append(i)
return alpha_eq_0_index
compute_time_nondim(total_forces)
alpha_eq_0_index = compute_alpha_dot(total_forces)
print(f"Found {len(alpha_eq_0_index)} points where alpha = 0")
[09:57:54] INFO: using: SI unit system for unit inference.
Found 7 points where alpha = 0
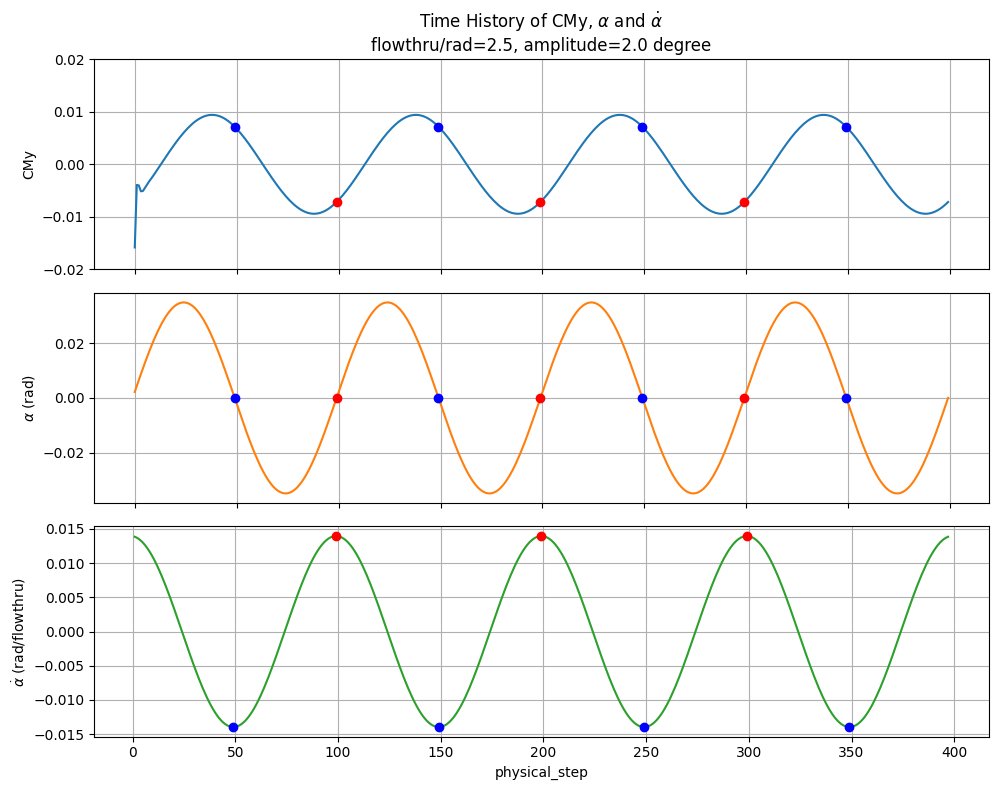
Plot time history#
Plot the time history of the pitch moment coefficient \(C_{My}\), angle of attack \(\alpha\), and pitch rate \(\dot{\alpha}\). The blue and red dots mark the points where \(\alpha = 0\) (extrema of \(\dot{\alpha}\)).
[10]:
def plot_time_history(df, alpha_eq_0_idx):
_, axs = plt.subplots(3, figsize=(10, 8))
# Time history of CMy
axs[0].plot(df["physical_step"], df["CMy"], color=cmap.colors[0])
axs[0].set_yticks(np.linspace(-0.02, 0.02, 5))
axs[0].set_ylim([-0.02, 0.02])
axs[0].set_ylabel("CMy")
# Time history of alpha
axs[1].plot(df["physical_step"], df["alpha"], color=cmap.colors[1])
axs[1].set_ylabel(r"$\alpha$ (rad)")
# Time history of alpha_dot
axs[2].plot(df["physical_step"][1:-2], df["alpha_dot"][1:-2], color=cmap.colors[2])
axs[2].set_ylabel(r"$\dot{\alpha}$ (rad/flowthru)")
axs[2].set_xlabel("physical_step")
for ax in axs:
ax.label_outer()
ax.grid()
# Mark alpha=0 points (blue for min alpha_dot, red for max alpha_dot)
for i in alpha_eq_0_idx:
color = "b" if df["alpha_dot"][i] < 0 else "r"
axs[0].plot(df["physical_step"][i], df["CMy"][i], "o", color=color)
axs[1].plot(df["physical_step"][i], df["alpha"][i], "o", color=color)
axs[2].plot(df["physical_step"][i], df["alpha_dot"][i], "o", color=color)
axs[0].set_title(
r"Time History of CMy, $\alpha$ and $\dot{\alpha}$"
+ "\n"
+ f"flowthru/rad={n_chord_per_period:.1f}, amplitude={amplitude_deg:.1f}"
)
plt.tight_layout()
plt.show()
plot_time_history(total_forces, alpha_eq_0_index)
Extract dynamic derivative#
Plot \(C_{My}\) vs \(\dot{\alpha}\) for the last oscillation period and compute the dynamic derivative \(\frac{dC_{My}}{dq}\) from linear regression at \(\alpha = 0\).
[11]:
def plot_CMy_vs_q(df, alpha_eq_0_idx):
plt.figure(figsize=(8, 6))
# Plot CMy versus alpha_dot for the last period
n_steps = len(df["physical_step"])
begin = n_steps - 201
end = n_steps - 1
alpha_dot = df.loc[begin:end, "alpha_dot"]
CMy = df.loc[begin:end, "CMy"]
plt.plot(alpha_dot, CMy, ".")
# Extract alpha=0 points in the last period
x = []
y = []
for i in alpha_eq_0_idx:
if i >= begin and i <= end:
x.append(df.loc[i, "alpha_dot"])
y.append(df.loc[i, "CMy"])
# Mark the alpha=0 points
plt.plot(x[0], y[0], "o", color="r", markersize=10)
plt.plot(x[1], y[1], "o", color="b", markersize=10)
# Linear regression through alpha=0 points
coef = np.polyfit(x, y, 1)
func = np.poly1d(coef)
x_line = np.linspace(-0.02, 0.02, 101)
plt.plot(x_line, func(x_line), "--", label=f"slope = {coef[0]:.3f}", color="k")
# Formatting
plt.xlabel(r"$\dot{\alpha} = q$ (deg/flowthru)")
plt.ylabel("CMy")
plt.ylim([-0.02, 0.02])
plt.yticks(np.linspace(-0.02, 0.02, 5))
plt.grid()
plt.legend(loc="lower left")
plt.title(
f"Dynamic Derivative dCMy/dq\nflowthru/rad={n_chord_per_period:.1f}, amplitude={amplitude_deg:.1f}"
)
# Set x-axis to deg/flowthru
tick_locations = np.linspace(-1, 1, 5) / 180 * np.pi
ax = plt.gca()
ax.set_xticks(
tick_locations, [f"{loc * 180 / np.pi:.1f}" for loc in tick_locations]
)
# Add text annotations
ax.text(
-0.016,
0.01,
r"$\alpha = 0$" + "\n" + r"min $\dot{\alpha}$",
fontsize=14,
color="b",
)
ax.text(
+0.012,
-0.014,
r"$\alpha = 0$" + "\n" + r"max $\dot{\alpha}$",
fontsize=14,
color="r",
)
plt.tight_layout()
plt.show()
print(f"\nDynamic derivative: dCMy/dq = {coef[0]:.3f}")
plot_CMy_vs_q(total_forces, alpha_eq_0_index)
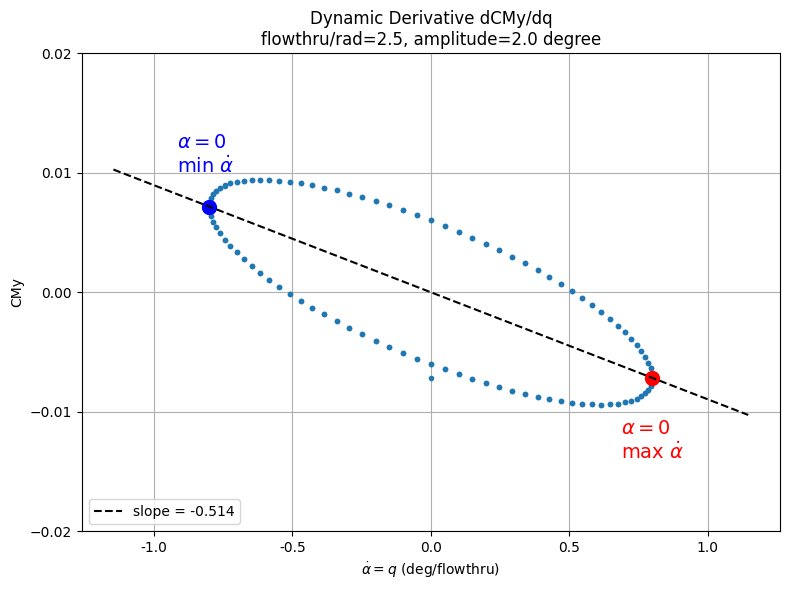
Dynamic derivative: dCMy/dq = -0.514
Summary#
This notebook demonstrated the complete workflow for calculating dynamic derivatives using Flow360:
Download Tutorial Files: Obtained the NACA0012 wing geometry (CSM format)
Create Project: Set up a Flow360 project from the geometry
Define Sliding Interface and Meshing: Configured the cylindrical sliding interface enclosing the wing, farfield zone, and mesh refinements
Run Steady Case: Initialized the flow field with a fixed sliding interface (zero angular velocity)
Understanding Oscillation Setup: Calculated nondimensional frequency and time step for sinusoidal pitching motion
Run Unsteady Case: Forked from steady solution and ran 400 time steps (4 complete cycles) with oscillating interface
Postprocessing: Extracted dynamic derivatives from force history
Extracted unique physical steps from force history
Computed angle of attack \(\alpha\) and pitch rate \(\dot{\alpha}\)
Extracted dynamic derivative from linear fit at \(\alpha = 0\)
Key Result: The dynamic pitching moment derivative is approximately:
This derivative is critical for:
Flight dynamics modeling
Stability and control analysis
Control system design
Aircraft certification