Dispersion calculation in tapered waveguide#
Integrated photonic waveguides provide a versatile platform for achieving a desired dispersion profile. By controlling the waveguide cross-section geometry, it is possible to obtain zero or near-zero waveguide dispersion across a wide range of wavelengths. This capability is crucial for various applications such as optical delay lines, modulators, and supercontinuum generators, as different spectral components associated with the propagation of short optical pulses can travel at different speeds
causing signal distortion. In this example, we will build a CMOS-compatible tapered waveguide presented in [1] N. Singh, D. Vermulen, A. Ruocco, N. Li, E. Ippen, F. X. Kärtner, and M. R. Watts. Supercontinuum generation in varying dispersion and birefringent silicon waveguide. Opt. Express 27(22), 31698-31712 (2019).DOI:10.1364/OE.27.031698, which demonstrates supercontinuum enhancement in varying dispersion waveguides. We will demonstrate how to
utilize the Tidy3D’s ModeSolver to compute the dispersion parameter (D) and the group-velocity dispersion (GVD) across the varying taper waveguide cross-section to replicate Figure 5 of [1].
For more integrated photonic waveguide examples such as the Dielectric waveguide with scale-invariant effective index, please visit our examples page.
If you are new to the finite-difference time-domain (FDTD) method, we highly recommend going through our FDTD101 tutorials. Details on using Tidy3D’s ModeSolver can be found here.
[1]:
import matplotlib.pyplot as plt
import numpy as np
import tidy3d as td
import tidy3d.web as web
from tidy3d.plugins import waveguide
from tidy3d.plugins.mode import ModeSolver
Tapered Waveguide#
The tapered waveguide is 5 mm long and varies adiabatically from 0.500 \(\mu m\) to 1.100 \(\mu m\) in width. The rib cross-section has a total height of 0.380 \(\mu m\) and a slab thickness of 0.065 \(\mu m\). The waveguide is etched into a silicon thin film and is surrounded by a thick silica layer.
[2]:
taper_w_in = 0.5 # Input taper width (um).
taper_w_out = 1.1 # Output taper width (um).
taper_l = 5000 # Taper length (um).
wg_h = 0.38 # Waveguide height (um).
wg_slab = 0.065 # Waveguide slab thickness (um).
The group-velocity dispersion (GVD) variation will be computed along the taper length at the wavelength of 1.95 \(\mu m\). In addition, we will calculate the dispersion parameter (D) between the wavelength range of 1.2 \(\mu m\) and 2.8 \(\mu m\).
[3]:
wl_min = 1.2 # Minimum wavelength in dispersion calculation.
wl_max = 2.4 # Maximum wavelength in dispersion calculation.
wl_steps = 21 # Number of wavelength points in mode calculation.
wl_d = np.linspace(wl_min, wl_max, wl_steps) # Wavelength range for D calculation.
wl_gvd = np.asarray([1.95]) # Wavelength for GVD calculation.
Simulation Setup#
Now, we will build the tapered waveguide structure using a `PolySlab <https://docs.flexcompute.com/projects/tidy3d/en/latest/api/_autosummary/tidy3d.PolySlab.html>`__ and materials taken from the material library.
[4]:
mat_si = td.material_library["cSi"]["Palik_Lossless"]
mat_sio2 = td.material_library["SiO2"]["Palik_Lossless"]
taper = td.Structure(
geometry=td.PolySlab(
vertices=[
[0, -taper_w_in / 2],
[taper_l, -taper_w_out / 2],
[taper_l, taper_w_out / 2],
[0, taper_w_in / 2],
],
axis=2,
slab_bounds=(-wg_h / 2, wg_h / 2),
),
medium=mat_si,
name="taper_core",
)
slab = td.Structure(
geometry=td.Box(center=[0, 0, -wg_h / 2 + wg_slab / 2], size=[td.inf, td.inf, wg_slab]),
medium=mat_si,
name="taper_slab",
)
sim = td.Simulation(
center=(taper_l / 2, 0, 0),
size=(1.1 * taper_l, taper_w_out + wl_max, 3),
grid_spec=td.GridSpec.auto(min_steps_per_wvl=15, wavelength=wl_min),
structures=[taper, slab],
run_time=1e-12,
medium=mat_sio2,
boundary_spec=td.BoundarySpec.all_sides(boundary=td.Periodic()),
symmetry=(0, -1, 0),
)
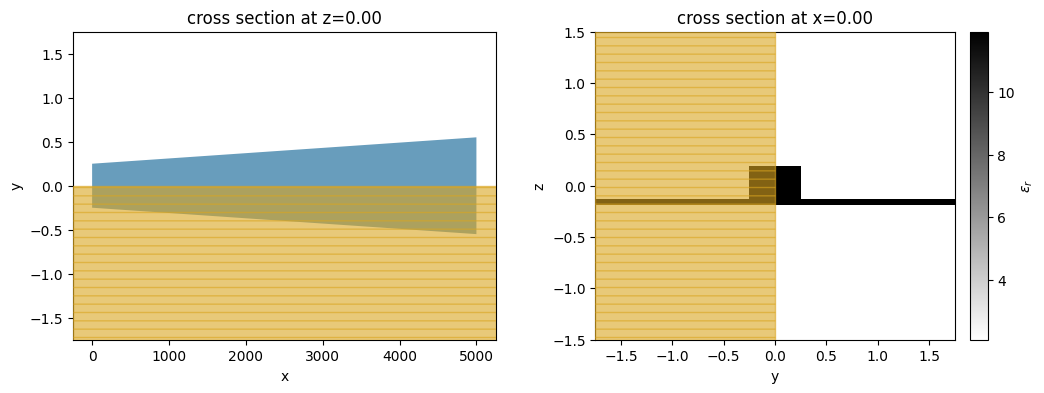
To ensure the simulation is correctly defined, we will visualize the permittivity distribution. As expected, we see the tapered waveguide profile along the x-direction and the rib cross-section in the yz plane.
[5]:
fig, ax = plt.subplots(1, 2, figsize=(12, 4))
sim.plot(z=0, ax=ax[0])
ax[0].set_aspect("auto")
sim.plot_eps(x=0, freq=td.C_0 / wl_gvd[0], ax=ax[1])
plt.show()
As we need to run the mode solver several times, we will create a helper function called build_mode. This function takes the arguments mode_pos_x, wl, num_modes, and group_index_step, and builds the ModeSolver. We plan to use this function to conduct a sweep on the mode plane position along the tapered waveguide to calculate the parameters D and GVD.
[6]:
def build_mode(
mode_pos_x: float = 0, wl: np.array = wl_d, num_modes: int = 1, group_index_step: float = 0.15
) -> ModeSolver:
"""Builds a ModeSolver object."""
freqs = td.C_0 / wl # Mode frequencies.
# Mode specification.
mode_spec = td.ModeSpec(
num_modes=num_modes,
group_index_step=group_index_step,
num_pml=[7, 7],
)
# Build a mode solver.
mode_solver = ModeSolver(
simulation=sim,
plane=td.Box(center=(mode_pos_x, 0, 0), size=(0, td.inf, td.inf)),
mode_spec=mode_spec,
freqs=freqs,
)
return mode_solver
Group Index Step Convergence#
According to [2] G. Agrawal. Nonlinear Fiber Optics (5th Ed.), Academic Press (2013), the effects of fiber dispersion are addressed by expanding the mode-propagation constant \(\beta\) in a Taylor series around the angular frequency \(\omega\). As a result, the parameters \(\beta_{1}\) and \(\beta_{2}\) are directly linked to the mode’s effective index \(n_{eff}(\omega)\) and its derivatives as
and
where \(c\) is the speed of light, \(v_{g}\) is the group velocity, and \(n_{g}\) is the group index. The first-order term \(\beta_{1}\) controls the speed at which the optical pulse envelope propagates, and the group velocity dispersion (GVD) parameter \(\beta_{2}\) represents dispersion of the group velocity and is responsible for pulse broadening. In practice, the dispersion parameter D, which is defined as \(d\beta_{1}/d\lambda\), is also used to quantify dispersion. It is related to \(\beta_{2}\) by
where \(\lambda\) is the light wavelength.
When calculating dispersion using the Tidy3D ModeSolver, additional frequency points are included to improve the accuracy of the effective index numerical differentiation. The parameter group_index_step controls the proximity of these additional frequency points to the user-supplied frequencies. Before proceeding with the main analyses, we will verify the convergence of our dispersion calculation with respect to the group_index_step parameter.
We will build a dictionary of ModeSolver instances to create a simulation batch as we run many mode solver calculations.
[7]:
# List of group_index_step values.
gis_values = [0.02, 0.05, 0.10, 0.15, 0.20]
# Mode sweep over the group_index_step values.
mode_gis = {}
for gis in gis_values:
mode_gis[f"gis={gis}"] = build_mode(mode_pos_x=taper_l / 2, group_index_step=gis)
Once the batch of ModeSolvers is created, we simply use the run() method to run the entire batch of tasks in parallel.
[8]:
# Run the mode solvers in parallel.
batch = web.Batch(simulations=mode_gis)
batch_gis = batch.run(path_dir="data")
22:19:48 CEST Started working on Batch containing 5 tasks.
22:19:54 CEST Maximum FlexCredit cost: 0.029 for the whole batch.
Use 'Batch.real_cost()' to get the billed FlexCredit cost after the Batch has completed.
22:19:59 CEST Batch complete.
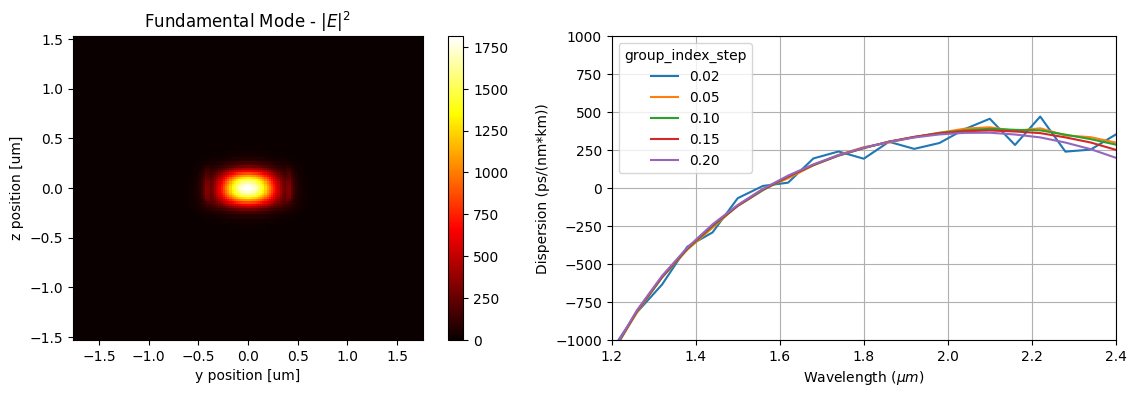
We can observe that a group_index_step value between 0.10 and 0.15 is enough to obtain a smooth dispersion curve, avoiding the numerical noise created in smaller group_index_step values.
[9]:
fig, ax = plt.subplots(1, 2, figsize=(12, 4), tight_layout=True)
batch_gis[f"gis={gis_values[0]}"].intensity.isel(
f=batch_gis[f"gis={gis_values[0]}"].modes_info["f"].size // 2, mode_index=0
).plot(x="y", y="z", cmap="hot", ax=ax[0])
ax[0].set_title("Fundamental Mode - $|E|^{2}$")
ax[0].set_aspect("equal")
for gis, md in batch_gis.items():
ax[1].plot(
td.C_0 / md.modes_info["f"].squeeze(drop=True).values,
md.modes_info["dispersion (ps/(nm km))"].squeeze(drop=True).values,
label=gis,
)
ax[1].set_ylabel("Dispersion (ps/(nm*km))")
ax[1].set_xlabel("Wavelength ($\\mu m$)")
ax[1].set_ylim([-1000, 1000])
ax[1].set_xlim([wl_d[0], wl_d[-1]])
ax[1].legend(title="group_index_step")
ax[1].grid()
plt.show()
Dispersion Parameters Calculation#
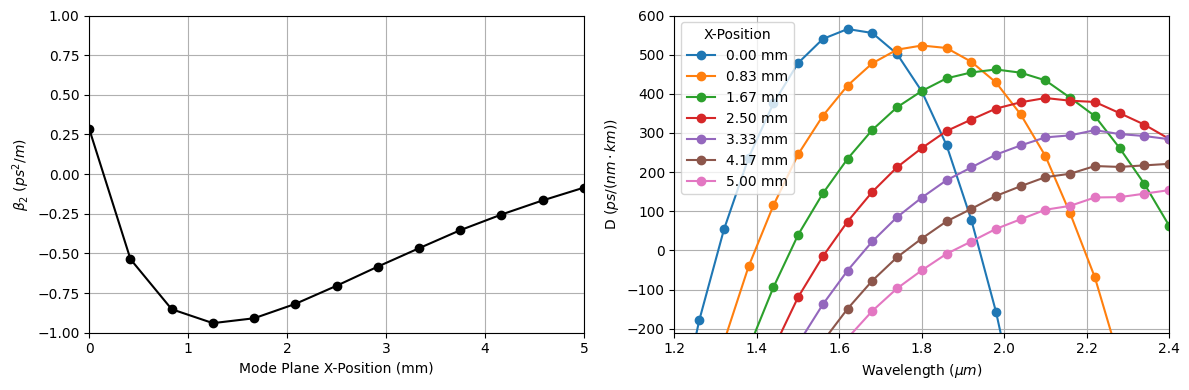
Now, we are ready to calculate the dispersion parameters for the varying waveguide cross-sections along the taper length. To reproduce Figure 5(a) of [1], we will calculate the \(\beta_{2}\) parameter of GVD at the wavelength of 1.95 \(\mu m\) for waveguide cross-sections ranging from 0.5 \(\mu m\) to 1.1 \(\mu m\) in intervals of 0.2 \(\mu m\).
[10]:
x_values_gvd = np.linspace(0.05, taper_l - 0.05, 13)
# Mode simulations to calculate beta2 of GVD.
mode_gvd = {}
for x in x_values_gvd:
mode_gvd[f"x={x:.2f}"] = build_mode(mode_pos_x=x, wl=wl_gvd, group_index_step=0.15)
[11]:
# Run the mode solvers in parallel.
batch = web.Batch(simulations=mode_gvd)
batch_gvd = batch.run(path_dir="data")
22:20:42 CEST Started working on Batch containing 13 tasks.
22:20:56 CEST Maximum FlexCredit cost: 0.048 for the whole batch.
Use 'Batch.real_cost()' to get the billed FlexCredit cost after the Batch has completed.
22:21:07 CEST Batch complete.
[12]:
# Mode simulations to calculate beta2 of GVD.
data_gvd = []
for _, md in batch_gvd.items():
d = md.modes_info["dispersion (ps/(nm km))"].squeeze(drop=True).values
beta2 = -((d * wl_gvd**2) / (2 * np.pi * td.C_0)) * 1e12
data_gvd.append(beta2)
Afterward, considering seven positions along the taper length, we will calculate the dispersion parameter D for wavelengths ranging from 1.2 \(\mu m\) to 2.4 \(\mu m\). We will use this data to plot Figure 5(b) of [1].
[13]:
x_values_d = np.linspace(0.05, taper_l - 0.05, 7)
# Mode simulations to calculate D.
mode_d = {}
for x in x_values_d:
mode_d[f"x={x:.2f}"] = build_mode(mode_pos_x=x, group_index_step=0.1)
[14]:
# Run the mode solvers in parallel.
batch = web.Batch(simulations=mode_d)
batch_d = batch.run(path_dir="data")
22:21:41 CEST Started working on Batch containing 7 tasks.
22:21:50 CEST Maximum FlexCredit cost: 0.041 for the whole batch.
Use 'Batch.real_cost()' to get the billed FlexCredit cost after the Batch has completed.
22:21:56 CEST Batch complete.
[15]:
data_d = []
for _, md in batch_d.items():
data_d.append(md.modes_info["dispersion (ps/(nm km))"].squeeze(drop=True).values)
Lastly, we will plot GVD and D dispersion parameters. We can observe a good agreement between the simulations and Figure 5(a-b).
[16]:
fig, ax = plt.subplots(1, 2, figsize=(12, 4), tight_layout=True)
# GVD
ax[0].plot(x_values_gvd / 1000, data_gvd, "ok-")
ax[0].set_ylabel("$\\beta_{2}$ ($ps^{2}/m$)")
ax[0].set_xlabel("Mode Plane X-Position (mm)")
ax[0].set_ylim([-1, 1])
ax[0].set_xlim([0, 5])
ax[0].grid()
# D
for l, d in zip(x_values_d, data_d):
ax[1].plot(wl_d, d, "-o", label=f"{l / 1000:.2f} mm")
ax[1].set_ylabel("D ($ps/(nm \\cdot km)$)")
ax[1].set_xlabel("Wavelength ($\\mu m$)")
ax[1].set_ylim([-210, 600])
ax[1].set_xlim([1.2, 2.4])
ax[1].legend(title="X-Position")
ax[1].grid()
plt.show()
[ ]: