Waveguide to ring coupling#
Optical ring resonators are key components in the field of integrated photonics. The unique capability of ring resonators to selectively interact with specific wavelengths of light makes them extremely versatile. They can be utilized in a broad array of applications, including optical filtering, modulating, switching, and sensing. However, simulating a ring resonator can be computationally expensive due to the high-Q resonances. Alternatively, we can investigate the coupling between a straight waveguide to a ring only by simulating the coupling region. The coupling coefficients can be extracted from this much simpler simulation.
Noticeably, in a waveguide-to-ring simulation, one of the simulation domain boundaries intersects the ring structure. Non-translational invariant structures inside PML are known to cause instabilities in a FDTD simulation so such a simulation is likely to diverge. In this notebook, we will try to use the PML boundary first to see if the simulation diverges. When it does, we will apply an effective remedy under this situation: replacing the PML with the adiabatic absorber boundary. The absorber functions similarly to PML such that it absorbs the outgoing radiation to mimic the infinite space. However, the absorber has a slightly higher reflection and requires a bit more computation than PML but it is numerically much more stable.
FDTD simulations can diverge due to various reasons. If you run into any simulation divergence issues, please follow the steps outlined in our troubleshooting guide to resolve it.

For more integrated photonic examples such as the 8-Channel mode and polarization de-multiplexer, the broadband bi-level taper polarization rotator-splitter, and the broadband directional coupler, please visit our examples page.
If you are new to the finite-difference time-domain (FDTD) method, we highly recommend going through our FDTD101 tutorials.
[1]:
import numpy as np
import matplotlib.pyplot as plt
import gdstk
import tidy3d as td
import tidy3d.web as web
Simulation Setup#
Define simulation wavelength range to be 1.5 \(\mu m\) to 1.6 \(\mu m\). .
[2]:
lda0 = 1.55 # central wavelength
ldas = np.linspace(1.5, 1.6, 101) # wavelength range of interest
freq0 = td.C_0 / lda0 # central frequency
freqs = td.C_0 / ldas # frequency range of interest
fwidth = 0.5 * (np.max(freqs) - np.min(freqs)) # frequency width of the source
The ring and waveguide are made of silicon. The top and bottom claddings are made of silicon oxide. Here we use the materials from Tidy3D’s material library directly.
[3]:
# define silicon and silicon dioxide media from the material library
si = td.material_library["cSi"]["Li1993_293K"]
sio2 = td.material_library["SiO2"]["Horiba"]
Define the geometric parameters. The waveguide is 500 nm wide and 220 nm thick. The ring has a radius of 5 \(\mu m\) and the gap size is 50 nm.
[4]:
w = 0.5 # width of the waveguide
h_si = 0.22 # thickness of the silicon layer
gap = 0.05 # gap size between the waveguides and the ring
r = 5 # radius of the ring
inf_eff = 1e2 # effective infinity
# simulation domain size
Lx = 2 * r + 2 * lda0
Ly = r / 2 + gap + 2 * w + lda0
Lz = 9 * h_si
We only need to define two structures: a straight waveguide and a ring. Both are commonly used PIC components introduced in the demonstration notebook. We can simply copy the associated functions here and them use to define the structures quickly. Namely, we copy the straight_waveguide function and the ring_resonator function.
[5]:
def straight_waveguide(x0, y0, z0, x1, y1, wg_width, wg_thickness, medium, sidewall_angle=0):
"""
This function defines a straight strip waveguide and returns the tidy3d structure of it.
Parameters
----------
x0: x coordinate of the waveguide starting position (um)
y0: y coordinate of the waveguide starting position (um)
z0: z coordinate of the waveguide starting position (um)
x1: x coordinate of the waveguide end position (um)
y1: y coordinate of the waveguide end position (um)
wg_width: width of the waveguide (um)
wg_thickness: thickness of the waveguide (um)
medium: medium of the waveguide
sidewall_angle: side wall angle of the waveguide (rad)
"""
cell = gdstk.Cell("waveguide") # define a gds cell
path = gdstk.RobustPath((x0, y0), wg_width, layer=1, datatype=0) # define a path
path.segment((x1, y1))
cell.add(path) # add path to the cell
# define geometry from the gds cell
wg_geo = td.PolySlab.from_gds(
cell,
gds_layer=1,
axis=2,
slab_bounds=(z0 - wg_thickness / 2, z0 + wg_thickness / 2),
sidewall_angle=sidewall_angle,
)
# define tidy3d structure of the bend
wg = td.Structure(geometry=wg_geo[0], medium=medium)
return wg
[6]:
def ring_resonator(
x0,
y0,
z0,
R,
wg_width,
wg_thickness,
medium,
sidewall_angle=0,
):
"""
This function defines a ring and returns the tidy3d structure of it.
Parameters
----------
x0: x coordinate of center of the ring (um)
y0: y coordinate of center of the ring (um)
z0: z coordinate of center of the ring (um)
R: radius of the ring (um)
wg_width: width of the waveguide (um)
wg_thickness: thickness of the waveguide (um)
medium: medium of the waveguide
sidewall_angle: side wall angle of the waveguide (rad)
"""
cell = gdstk.Cell("top") # define a gds cell
# define a path
path_top = gdstk.RobustPath(
(x0 + R, y0), wg_width - wg_thickness * np.tan(np.abs(sidewall_angle)), layer=1, datatype=0
)
path_top.arc(R, 0, np.pi) # make the top half of the ring
cell.add(path_top) # add path to the cell
# the reference plane depends on the sign of the sidewall_angle
if sidewall_angle >= 0:
reference_plane = "top"
else:
reference_plane = "bottom"
# define top half ring geometry
ring_top_geo = td.PolySlab.from_gds(
cell,
gds_layer=1,
axis=2,
slab_bounds=(z0 - wg_thickness / 2, z0 + wg_thickness / 2),
sidewall_angle=sidewall_angle,
reference_plane=reference_plane,
)
# similarly for the bottom half of the ring
cell = gdstk.Cell("bottom")
path_bottom = gdstk.RobustPath(
(x0 + R, y0), wg_width - wg_thickness * np.tan(np.abs(sidewall_angle)), layer=1, datatype=0
)
path_bottom.arc(R, 0, -np.pi)
cell.add(path_bottom)
ring_bottom_geo = td.PolySlab.from_gds(
cell,
gds_layer=1,
axis=2,
slab_bounds=(z0 - wg_thickness / 2, z0 + wg_thickness / 2),
sidewall_angle=sidewall_angle,
reference_plane=reference_plane,
)
# define ring structure
ring = td.Structure(
geometry=td.GeometryGroup(geometries=ring_bottom_geo + ring_top_geo), medium=medium
)
return ring
Use the above functions to define the Structures.
[7]:
# define straight waveguide
waveguide = straight_waveguide(
x0=-inf_eff,
y0=0,
z0=0,
x1=inf_eff,
y1=0,
wg_width=w,
wg_thickness=h_si,
medium=si,
sidewall_angle=0,
)
# define ring
ring = ring_resonator(
x0=0,
y0=w + gap + r,
z0=0,
R=r,
wg_width=w,
wg_thickness=h_si,
medium=si,
sidewall_angle=0,
)
We will use a ModeSource to excite the straight waveguide using the fundamental TE mode. A ModeMonitor is placed at the through to measure the transmission. Another ModeMonitor is placed at the ring to measure the coupling to the ring. For the monitor at the ring, we need to properly set up angle_theta, angle_theta, and bend_axis in the
ModeSpec as demonstrated in the tutorial. Finally, we add a FieldMonitor to help visualize the field distribution.
[8]:
n_si = 3.47
# mode spec for the source
mode_spec_source = td.ModeSpec(num_modes=1, target_neff=n_si)
# mode spec for the through port
mode_spec_through = mode_spec_source
# angle of the mode at the ring
theta = np.pi / 4
# mode spec for the drop port at the ring
mode_spec_drop = td.ModeSpec(
num_modes=1, target_neff=n_si, angle_theta=theta, bend_radius=-r, bend_axis=1
)
# add a mode source as excitation
mode_source = td.ModeSource(
center=(-r - lda0 / 4, 0, 0),
size=(0, 6 * w, 6 * h_si),
source_time=td.GaussianPulse(freq0=freq0, fwidth=fwidth),
direction="+",
mode_spec=mode_spec_source,
mode_index=0,
)
# add a mode monitor to measure transmission at the through port
mode_monitor_through = td.ModeMonitor(
center=(r + lda0 / 4, 0, 0),
size=mode_source.size,
freqs=freqs,
mode_spec=mode_spec_through,
name="through",
)
# add a mode monitor to measure transmission at the drop port
mode_monitor_drop = td.ModeMonitor(
center=(np.sin(theta) * r, w + gap + r - np.cos(theta) * r, 0),
size=(6 * w, 0, 6 * h_si),
freqs=freqs,
mode_spec=mode_spec_drop,
name="drop",
)
# add a field monitor to visualize the field distribution
field_monitor = td.FieldMonitor(
center=(0, 0, 0), size=(td.inf, td.inf, 0), freqs=[freq0], name="field"
)
[18:57:43] WARNING: Default value for the field monitor monitor.py:261 'colocate' setting has changed to 'True' in Tidy3D 2.4.0. All field components will be colocated to the grid boundaries. Set to 'False' to get the raw fields on the Yee grid instead.
Using PML Boundary#
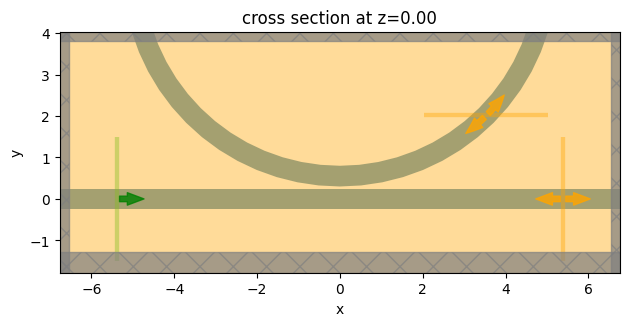
Finally, we define the Simulation. Intuitively, we would use the PML boundary on all sides similar to what we did in most other PIC component simulations. Let’s try it here.
[9]:
run_time = 2e-12 # simulation run time
# construct simulation
sim_pml = td.Simulation(
center=(0, Ly / 4, 0),
size=(Lx, Ly, Lz),
grid_spec=td.GridSpec.auto(min_steps_per_wvl=25, wavelength=lda0),
structures=[waveguide, ring],
sources=[mode_source],
monitors=[mode_monitor_through, mode_monitor_drop, field_monitor],
run_time=run_time,
boundary_spec=td.BoundarySpec.all_sides(boundary=td.PML()),
medium=sio2,
symmetry=(0, 0, 1),
)
# plot simulation
sim_pml.plot(z=0)
plt.show()
/home/momchil/miniconda3/envs/tidy3d-docs/lib/python3.9/site-packages/shapely/set_operations.py:133: RuntimeWarning: invalid value encountered in intersection
return lib.intersection(a, b, **kwargs)
Submit the simulation to the server to run.
[10]:
sim_data = web.run(
simulation=sim_pml, task_name="waveguide_to_ring", path="data/simulation_data.hdf5"
)
View task using web UI at webapi.py:190 'https://tidy3d.simulation.cloud/workbench?taskId=fdve- 36b213bb-ae23-4827-ab34-b31816ebae25v1'.
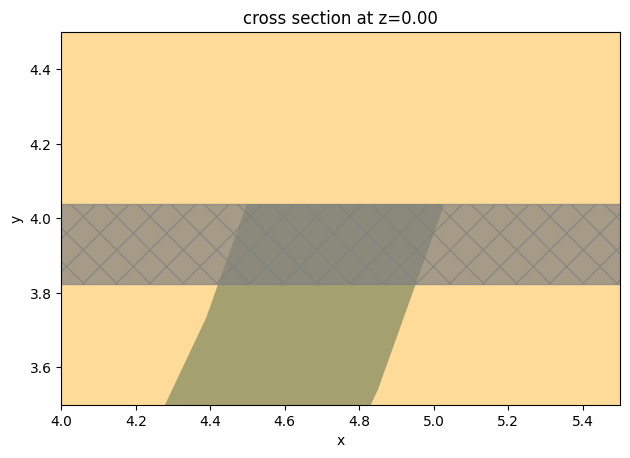
Now we see that the status of the job is shown to be diverged. As discussed in the introduction, it should not come as a surprise since the ring section in the PML layer is not perpendicular to the boundary and translational invariant as shown in the zoomed-in plot below.
[11]:
# zoom-in plot around the pml
ax = sim_pml.plot(z=0)
ax.set_xlim(4, 5.5)
ax.set_ylim(3.5, 4.5)
plt.show()
/home/momchil/miniconda3/envs/tidy3d-docs/lib/python3.9/site-packages/shapely/set_operations.py:133: RuntimeWarning: invalid value encountered in intersection
return lib.intersection(a, b, **kwargs)
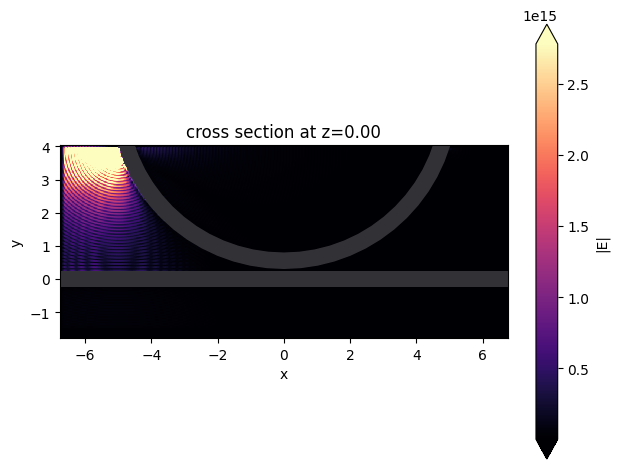
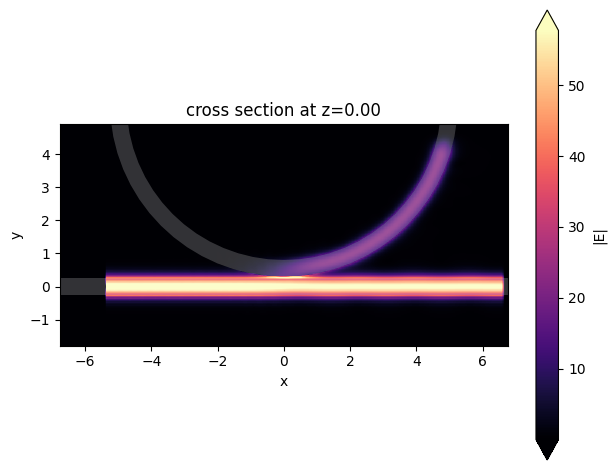
This can be further confirmed by plotting the electric field distribution. From the plot, we can see where the field built up and caused the simulation to diverge. As expected, the field built up around the ring to PML area.
[12]:
sim_data.plot_field(field_monitor_name="field", field_name="E", val="abs")
plt.show()
Using Absorber Boundary#
To resolve the diverge, we can switch to Absorber. This can be done by copying the previous simulation and only updating the boundary_spec. Since the ring is only intersecting the boundary in the y direction, we only need to apply Absorber to the positive \(y\) boundary.
In addition, we increased the number of layers in the Absorber to 60 to ensure sufficient absorption and minimal reflection.
[13]:
# copy simulation and update boundary condition
sim_absorber = sim_pml.copy(
update={
"boundary_spec": td.BoundarySpec(
x=td.Boundary.pml(),
y=td.Boundary(plus=td.Absorber(num_layers=60), minus=td.PML()),
z=td.Boundary.pml(),
)
}
)
# run simulation
sim_data = web.run(
simulation=sim_absorber, task_name="waveguide_to_ring", path="data/simulation_data.hdf5"
)
View task using web UI at webapi.py:190 'https://tidy3d.simulation.cloud/workbench?taskId=fdve- f78250d4-0834-42a9-92e0-d47037b0bab1v1'.
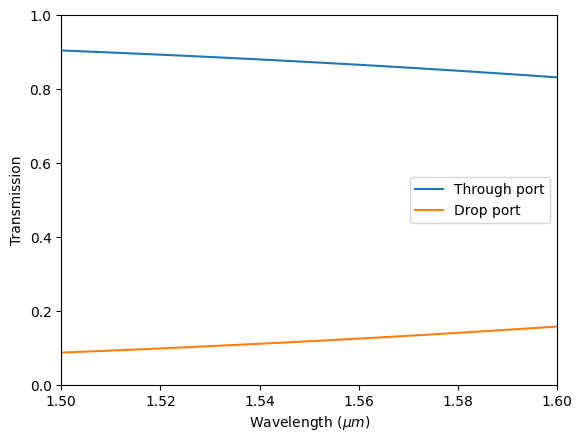
After switching to Absorber, the simulation doesn’t run into the divergence issue anymore and thus we can plot the transmission spectra to the through and drop ports.
[14]:
# extract mode amplitude in the through port
t = sim_data["through"].amps.sel(mode_index=0, direction="+")
# extract mode amplitude in the drop port
k = sim_data["drop"].amps.sel(mode_index=0, direction="+")
# plot transmission
plt.plot(ldas, np.abs(t) ** 2, label="Through port")
plt.plot(ldas, np.abs(k) ** 2, label="Drop port")
plt.legend()
plt.xlabel("Wavelength ($\mu m$)")
plt.ylabel("Transmission")
plt.xlim(1.5, 1.6)
plt.ylim(0, 1)
plt.show()
Again we can visualize the field distribution. This time, we see the correct result where the energy is partially coupled to the ring and partially stays in the straight waveguide.
[15]:
sim_data.plot_field(field_monitor_name="field", field_name="E", val="abs")
plt.show()
Additional Notes on Absorber#
The adiabatic absorber is a multilayer system with gradually increasing conductivity. As briefly discussed above, the absorber usually has a larger undesired reflection compared to PML. In practice, this small difference rarely matters, but is important to understand for simulations that require high accuracy. There are two possible sources for the reflection from absorbers. The first, and more common one, is that the ramping up of the conductivity is not sufficiently slow, which can be remedied
by increasing the number of absorber layers (40 by default). The second one is that the absorption is not high enough, such that the light reaches the PEC boundary at the end of the Absorber, travels back through it, and is still not fully attenuated before re-entering the simulation region. If this is the case, increasing the maximum conductivity (see the API reference) can help. In both cases, changing the order of the scaling of the conductivity
(sigma_order) can also have an effect, but this is a more advanced setting that we typically do not recommend modifying.
[ ]:
