tidy3d.Simulation

tidy3d.Simulation#

class Simulation[source]#

Bases: AbstractSimulation

Custom implementation of Maxwell’s equations which represents the physical model to be solved using the FDTD method.

Parameters:

center (Attribute: center) –

Type

Tuple[float, float, float]

Default

= (0.0, 0.0, 0.0)

Units

um

Description

Center of object in x, y, and z.
size (Attribute: size) –

Type

Tuple[NonNegativeFloat, NonNegativeFloat, NonNegativeFloat]

Default

Units

um

Description

Size in x, y, and z directions.

medium (Attribute: medium) –

`Type`	Union[Medium, AnisotropicMedium, PECMedium, PoleResidue, Sellmeier, Lorentz, Debye, Drude, FullyAnisotropicMedium, CustomMedium, CustomPoleResidue, CustomSellmeier, CustomLorentz, CustomDebye, CustomDrude, CustomAnisotropicMedium, PerturbationMedium, PerturbationPoleResidue]
`Default`	= Medium(nameNone, frequency_rangeNone, allow_gainFalse, nonlinear_specNone, modulation_specNone, heat_specNone, type’Medium’, permittivity1.0, conductivity0.0)
`Description`	Background medium of simulation, defaults to vacuum if not specified.

structures (Attribute: structures) –

`Type`	Tuple[Structure, …]
`Default`	= ()
`Description`	Tuple of structures present in simulation. Note: Structures defined later in this list override the simulation material properties in regions of spatial overlap.

symmetry (Attribute: symmetry) –

`Type`	Tuple[Literal[0, -1, 1], Literal[0, -1, 1], Literal[0, -1, 1]]
`Default`	= (0, 0, 0)
`Description`	Tuple of integers defining reflection symmetry across a plane bisecting the simulation domain normal to the x-, y-, and z-axis at the simulation center of each axis, respectively. Each element can be `0` (no symmetry), `1` (even, i.e. ‘PMC’ symmetry) or `-1` (odd, i.e. ‘PEC’ symmetry). Note that the vectorial nature of the fields must be taken into account to correctly determine the symmetry value.

sources (Attribute: sources) –

`Type`	Tuple[Annotated[Union[tidy3d.components.source.UniformCurrentSource, tidy3d.components.source.PointDipole, tidy3d.components.source.GaussianBeam, tidy3d.components.source.AstigmaticGaussianBeam, tidy3d.components.source.ModeSource, tidy3d.components.source.PlaneWave, tidy3d.components.source.CustomFieldSource, tidy3d.components.source.CustomCurrentSource, tidy3d.components.source.TFSF], FieldInfo(default=PydanticUndefined, discriminator=’type’, extra={})], …]
`Default`	= ()
`Description`	Tuple of electric current sources injecting fields into the simulation.

boundary_spec (Attribute: boundary_spec) –

`Type`	BoundarySpec
`Default`	= BoundarySpec(xBoundary(plusPML(nameNone,, type’PML’,, num_layers12,, parametersPMLParams(sigma_order3,, sigma_min0.0,, sigma_max1.5,, type’PMLParams’,, kappa_order3,, kappa_min1.0,, kappa_max3.0,, alpha_order1,, alpha_min0.0,, alpha_max0.0)),, minusPML(nameNone,, type’PML’,, num_layers12,, parametersPMLParams(sigma_order3,, sigma_min0.0,, sigma_max1.5,, type’PMLParams’,, kappa_order3,, kappa_min1.0,, kappa_max3.0,, alpha_order1,, alpha_min0.0,, alpha_max0.0)),, type’Boundary’), yBoundary(plusPML(nameNone,, type’PML’,, num_layers12,, parametersPMLParams(sigma_order3,, sigma_min0.0,, sigma_max1.5,, type’PMLParams’,, kappa_order3,, kappa_min1.0,, kappa_max3.0,, alpha_order1,, alpha_min0.0,, alpha_max0.0)),, minusPML(nameNone,, type’PML’,, num_layers12,, parametersPMLParams(sigma_order3,, sigma_min0.0,, sigma_max1.5,, type’PMLParams’,, kappa_order3,, kappa_min1.0,, kappa_max3.0,, alpha_order1,, alpha_min0.0,, alpha_max0.0)),, type’Boundary’), zBoundary(plusPML(nameNone,, type’PML’,, num_layers12,, parametersPMLParams(sigma_order3,, sigma_min0.0,, sigma_max1.5,, type’PMLParams’,, kappa_order3,, kappa_min1.0,, kappa_max3.0,, alpha_order1,, alpha_min0.0,, alpha_max0.0)),, minusPML(nameNone,, type’PML’,, num_layers12,, parametersPMLParams(sigma_order3,, sigma_min0.0,, sigma_max1.5,, type’PMLParams’,, kappa_order3,, kappa_min1.0,, kappa_max3.0,, alpha_order1,, alpha_min0.0,, alpha_max0.0)),, type’Boundary’), type’BoundarySpec’)
`Description`	Specification of boundary conditions along each dimension. If `None`, PML boundary conditions are applied on all sides.

monitors (Attribute: monitors) –

`Type`	Tuple[Annotated[Union[tidy3d.components.monitor.FieldMonitor, tidy3d.components.monitor.FieldTimeMonitor, tidy3d.components.monitor.PermittivityMonitor, tidy3d.components.monitor.FluxMonitor, tidy3d.components.monitor.FluxTimeMonitor, tidy3d.components.monitor.ModeMonitor, tidy3d.components.monitor.ModeSolverMonitor, tidy3d.components.monitor.FieldProjectionAngleMonitor, tidy3d.components.monitor.FieldProjectionCartesianMonitor, tidy3d.components.monitor.FieldProjectionKSpaceMonitor, tidy3d.components.monitor.DiffractionMonitor], FieldInfo(default=PydanticUndefined, discriminator=’type’, extra={})], …]
`Default`	= ()
`Description`	Tuple of monitors in the simulation. Note: monitor names are used to access data after simulation is run.

grid_spec (Attribute: grid_spec) –

`Type`	GridSpec
`Default`	= GridSpec(grid_xAutoGrid(type’AutoGrid’,, min_steps_per_wvl10.0,, max_scale1.4,, dl_min0.0,, mesherGradedMesher(type’GradedMesher’)), grid_yAutoGrid(type’AutoGrid’,, min_steps_per_wvl10.0,, max_scale1.4,, dl_min0.0,, mesherGradedMesher(type’GradedMesher’)), grid_zAutoGrid(type’AutoGrid’,, min_steps_per_wvl10.0,, max_scale1.4,, dl_min0.0,, mesherGradedMesher(type’GradedMesher’)), wavelengthNone, override_structures(), type’GridSpec’)
`Description`	Specifications for the simulation grid along each of the three directions.

version (Attribute: version) –

Type

str

Default

= 2.6.0rc1

Description

String specifying the front end version number.

run_time (Attribute: run_time) –

`Type`	PositiveFloat
`Default`
`Units`	sec
`Description`	Total electromagnetic evolution time in seconds. Note: If simulation ‘shutoff’ is specified, simulation will terminate early when shutoff condition met.

shutoff (Attribute: shutoff) –

`Type`	NonNegativeFloat
`Default`	= 1e-05
`Description`	Ratio of the instantaneous integrated E-field intensity to the maximum value at which the simulation will automatically terminate time stepping. Used to prevent extraneous run time of simulations with fully decayed fields. Set to `0` to disable this feature.

subpixel (Attribute: subpixel) –

Type

bool

Default

= True

Description

If True, uses subpixel averaging of the permittivity based on structure definition, resulting in much higher accuracy for a given grid size.

normalize_index (Attribute: normalize_index) –

`Type`	Optional[NonNegativeInt]
`Default`	= 0
`Description`	Index of the source in the tuple of sources whose spectrum will be used to normalize the frequency-dependent data. If `None`, the raw field data is returned unnormalized.

courant (Attribute: courant) –

`Type`	ConstrainedFloatValue
`Default`	= 0.99
`Description`	Courant stability factor, controls time step to spatial step ratio. Lower values lead to more stable simulations for dispersive materials, but result in longer simulation times. This factor is normalized to no larger than 1 when CFL stability condition is met in 3D.

Notes

A Simulation defines a custom implementation of Maxwell’s equations which represents the physical model to be solved using the Finite-Difference Time-Domain (FDTD) method. tidy3d simulations run very quickly in the cloud through GPU parallelization.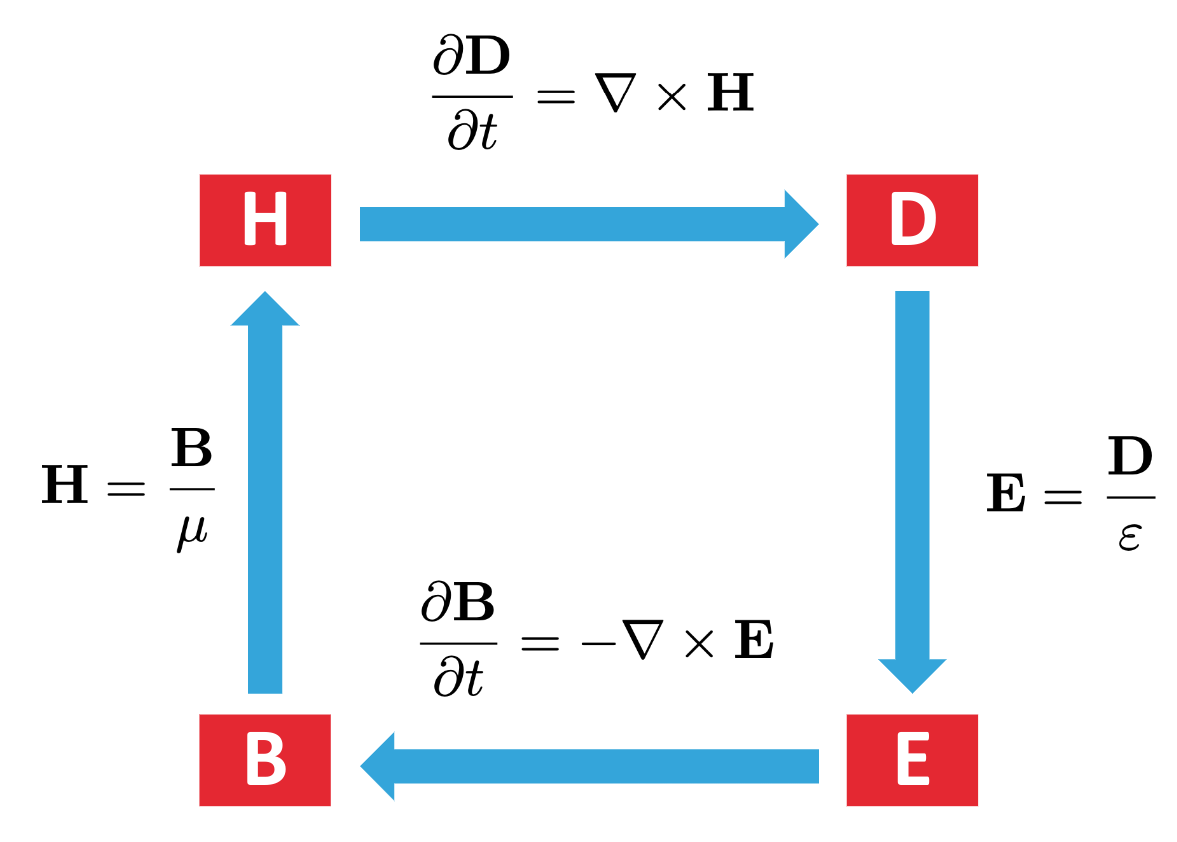

FDTD is a method for simulating the interaction of electromagnetic waves with structures and materials. It is the most widely used method in photonics design. The Maxwell’s equations implemented in the Simulation are solved per time-step in the order shown in this image.

The simplified input to FDTD solver consists of the permittivity distribution defined by structures which describe the device and sources of electromagnetic excitation. This information is used to computate the time dynamics of the electric and magnetic fields in this system. From these time-domain results, frequency-domain information of the simulation can also be extracted, and used for device design and optimization.

If you are new to the FDTD method, we recommend you get started with the FDTD 101 Lecture Series

Dimensions Selection

By default, simulations are defined as 3D. To make the simulation 2D, we can just set the simulation size in one of the dimensions to be 0. However, note that we still have to define a grid size (eg. tidy3d.Simulation(size=[size_x, size_y, 0])) and specify a periodic boundary condition in that direction.

See further parameter explanations below.

Example

>>> from tidy3d import Sphere, Cylinder, PolySlab
>>> from tidy3d import UniformCurrentSource, GaussianPulse
>>> from tidy3d import FieldMonitor, FluxMonitor
>>> from tidy3d import GridSpec, AutoGrid
>>> from tidy3d import BoundarySpec, Boundary
>>> sim = Simulation(
...     size=(3.0, 3.0, 3.0),
...     grid_spec=GridSpec(
...         grid_x = AutoGrid(min_steps_per_wvl = 20),
...         grid_y = AutoGrid(min_steps_per_wvl = 20),
...         grid_z = AutoGrid(min_steps_per_wvl = 20)
...     ),
...     run_time=40e-11,
...     structures=[
...         Structure(
...             geometry=Box(size=(1, 1, 1), center=(0, 0, 0)),
...             medium=Medium(permittivity=2.0),
...         ),
...     ],
...     sources=[
...         UniformCurrentSource(
...             size=(0, 0, 0),
...             center=(0, 0.5, 0),
...             polarization="Hx",
...             source_time=GaussianPulse(
...                 freq0=2e14,
...                 fwidth=4e13,
...             ),
...         )
...     ],
...     monitors=[
...         FluxMonitor(size=(1, 1, 0), center=(0, 0, 0), freqs=[2e14, 2.5e14], name='flux'),
...     ],
...     symmetry=(0, 0, 0),
...     boundary_spec=BoundarySpec(
...         x = Boundary.pml(num_layers=20),
...         y = Boundary.pml(num_layers=30),
...         z = Boundary.periodic(),
...     ),
...     shutoff=1e-6,
...     courant=0.8,
...     subpixel=False,
... )

See also

Notebooks:

Quickstart: Usage in a basic simulation flow.
Using automatic nonuniform meshing
See nearly all notebooks for Simulation applications.

Lectures:

Introduction to FDTD Simulation: Usage in a basic simulation flow.
Prelude to Integrated Photonics Simulation: Mode Injection

GUI:

FDTD Walkthrough

Attributes

`allow_gain`	`True` if any of the mediums in the simulation allows gain.
`background_structure`	Returns structure representing the background of the `Simulation`.
`bounds_pml`	Simulation bounds including the PML regions.
`complex_fields`	Whether complex fields are used in the simulation.
`custom_datasets`	List of custom datasets for verification purposes.
`dt`	Simulation time step (distance).
`frequency_range`	Range of frequencies spanning all sources' frequency dependence.
`grid`	FDTD grid spatial locations and information.
`medium_map`	Returns dict mapping medium to index in material.
`mediums`	Returns set of distinct `AbstractMedium` in simulation.
`monitors_data_size`	Dictionary mapping monitor names to their estimated storage size in bytes.
`num_cells`	Number of cells in the simulation.
`num_pml_layers`	Number of absorbing layers in all three axes and directions (-, +).
`num_time_steps`	Number of time steps in simulation.
`nyquist_step`	Maximum number of discrete time steps to keep sampling below Nyquist limit.
`pml_thicknesses`	Thicknesses (um) of absorbers in all three axes and directions (-, +)
`simulation_bounds`	Simulation bounds including the PML regions.
`tmesh`	FDTD time stepping points.
`volumetric_structures`	Generate a tuple of structures wherein any 2D materials are converted to 3D volumetric equivalents.
`wvl_mat_min`	Minimum wavelength in the material.
`version`	Defines the front end version of tidy3d

Methods

`bloch_with_symmetry`(val, values)	Error if a Bloch boundary is applied with symmetry
`boundaries_for_zero_dims`(val, values)	Error if absorbing boundaries, unmatching pec/pmc, or symmetry is used along a zero dimension.
`diffraction_monitor_boundaries`(val, values)	If any `DiffractionMonitor` exists, ensure boundary conditions in the transverse directions are periodic or Bloch.
`diffraction_monitor_medium`(val, values)	If any `DiffractionMonitor` exists, ensure is does not lie in a lossy medium.
`discretize`(box[, extend])	Grid containing only cells that intersect with a `Box`.
`discretize_monitor`(monitor)	Grid on which monitor data corresponding to a given monitor will be computed.
`eps_bounds`([freq])	Compute range of (real) permittivity present in the simulation at frequency "freq".
`epsilon`(box[, coord_key, freq])	Get array of permittivity at volume specified by box and freq.
`epsilon_on_grid`(grid[, coord_key, freq])	Get array of permittivity at a given freq on a given grid.
`from_scene`(scene, **kwargs)	Create a simulation from a `Scene` instance.
`intersecting_media`(test_object, structures)	From a given list of structures, returns a list of `AbstractMedium` associated with those structures that intersect with the `test_object`, if it is a surface, or its surfaces, if it is a volume.
`intersecting_structures`(test_object, structures)	From a given list of structures, returns a list of `Structure` that intersect with the `test_object`, if it is a surface, or its surfaces, if it is a volume.
`monitor_medium`(monitor)	Return the medium in which the given monitor resides.
`perturbed_mediums_copy`([temperature, ...])	Return a copy of the simulation with heat and/or charge data applied to all mediums that have perturbation models specified.
`plane_wave_boundaries`(val, values)	Error if there are plane wave sources incompatible with boundary conditions.
`plot`([x, y, z, ax, source_alpha, ...])	Plot each of simulation's components on a plane defined by one nonzero x,y,z coordinate.
`plot_3d`([width, height])	Render 3D plot of `Simulation` (in jupyter notebook only).
`plot_boundaries`([x, y, z, ax])	Plot the simulation boundary conditions as lines on a plane
`plot_eps`([x, y, z, freq, alpha, ...])	Plot each of simulation's components on a plane defined by one nonzero x,y,z coordinate.
`plot_grid`([x, y, z, ax, hlim, vlim])	Plot the cell boundaries as lines on a plane defined by one nonzero x,y,z coordinate.
`plot_pml`([x, y, z, hlim, vlim, ax])	Plot each of simulation's absorbing boundaries on a plane defined by one nonzero x,y,z coordinate.
`plot_structures_eps`([x, y, z, freq, alpha, ...])	Plot each of simulation's structures on a plane defined by one nonzero x,y,z coordinate.
`proj_distance_for_approx`(val, values)	Warn if projection distance for projection monitors is not large compared to monitor or, simulation size, yet far_field_approx is True.
`subsection`(region[, boundary_spec, ...])	Generate a simulation instance containing only the `region`.
`tfsf_boundaries`(val, values)	Error if the boundary conditions are compatible with TFSF sources, if any.
`tfsf_with_symmetry`(val, values)	Error if a TFSF source is applied with symmetry
`to_gds`(cell[, x, y, z, ...])	Append the simulation structures to a .gds cell.
`to_gds_file`(fname[, x, y, z, ...])	Append the simulation structures to a .gds cell.
`to_gdspy`([x, y, z, gds_layer_dtype_map])	Convert a simulation's planar slice to a .gds type polygon list.
`to_gdstk`([x, y, z, permittivity_threshold, ...])	Convert a simulation's planar slice to a .gds type polygon list.
`validate_pre_upload`([source_required])	Validate the fully initialized simulation is ok for upload to our servers.

run_time#

Total electromagnetic evolution time in seconds. If simulation ‘shutoff’ is specified, simulation will terminate early when shutoff condition met.

How long to run a simulation?

The frequency-domain response obtained in the FDTD simulation only accurately represents the continuous-wave response of the system if the fields at the beginning and at the end of the time stepping are (very close to) zero. So, you should run the simulation for a time enough to allow the electromagnetic fields decay to negligible values within the simulation domain.

When dealing with light propagation in a NON-RESONANT device, like a simple optical waveguide, a good initial guess to simulation run_time would be the a few times the largest domain dimension (\(L\)) multiplied by the waveguide mode group index (\(n_g\)), divided by the speed of light in a vacuum (\(c_0\)), plus the source_time:

\[t_{sim} \approx \frac{n_g L}{c_0} + t_{source}\]

By default, tidy3d checks periodically the total field intensity left in the simulation, and compares that to the maximum total field intensity recorded at previous times. If it is found that the ratio of these two values is smaller than the default shutoff value \(10^{-5}\), the simulation is terminated as the fields remaining in the simulation are deemed negligible. The shutoff value can be controlled using the shutoff parameter, or completely turned off by setting it to zero. In most cases, the default behavior ensures that results are correct, while avoiding unnecessarily long run times. The Flex Unit cost of the simulation is also proportionally scaled down when early termination is encountered.

Resonant Caveats

Should I make sure that fields have fully decayed by the end of the simulation?

The main use case in which you may want to ignore the field decay warning is when you have high-Q modes in your simulation that would require an extremely long run time to decay. In that case, you can use the the tidy3d.plugins.resonance.ResonanceFinder plugin to analyze the modes, as well as field monitors with vaporization to capture the modal profiles. The only thing to note is that the normalization of these modal profiles would be arbitrary, and would depend on the exact run time and apodization definition. An example of such a use case is presented in our case study.

See also

Notebooks

High-Q silicon resonator

sources#

Tuple of electric current sources injecting fields into the simulation.

Example

Simple application reference:

Simulation(
   ...
   sources=[
       UniformCurrentSource(
           size=(0, 0, 0),
           center=(0, 0.5, 0),
           polarization="Hx",
           source_time=GaussianPulse(
               freq0=2e14,
               fwidth=4e13,
           ),
       )
   ],
   ...
)

See also

Index:: Frequency and time domain source models.

boundary_spec#

Specification of boundary conditions along each dimension. If None, PML boundary conditions are applied on all sides.

Example

Simple application reference:

Simulation(
   ...
    boundary_spec=BoundarySpec(
       x = Boundary.pml(num_layers=20),
       y = Boundary.pml(num_layers=30),
       z = Boundary.periodic(),
   ),
   ...
)

See also

PML:

A perfectly matched layer model.

BoundarySpec:

Specifies boundary conditions on each side of the domain and along each dimension.

Index

All boundary condition models.

Notebooks

How to troubleshoot a diverged FDTD simulation

Lectures

Using FDTD to Compute a Transmission Spectrum

monitors#

Tuple of monitors in the simulation. Monitor names are used to access data after simulation is run.

See also

Index: All the monitor implementations.

grid_spec#

Specifications for the simulation grid along each of the three directions.

Example

Simple application reference:

Simulation(
   ...
    grid_spec=GridSpec(
       grid_x = AutoGrid(min_steps_per_wvl = 20),
       grid_y = AutoGrid(min_steps_per_wvl = 20),
       grid_z = AutoGrid(min_steps_per_wvl = 20)
   ),
   ...
)

Usage Recommendations

In the finite-difference time domain method, the computational domain is discretized by a little cubes called the Yee cell. A discrete lattice formed by this Yee cell is used to describe the fields. In 3D, the electric fields are distributed on the edge of the Yee cell and the magnetic fields are distributed on the surface of the Yee cell.

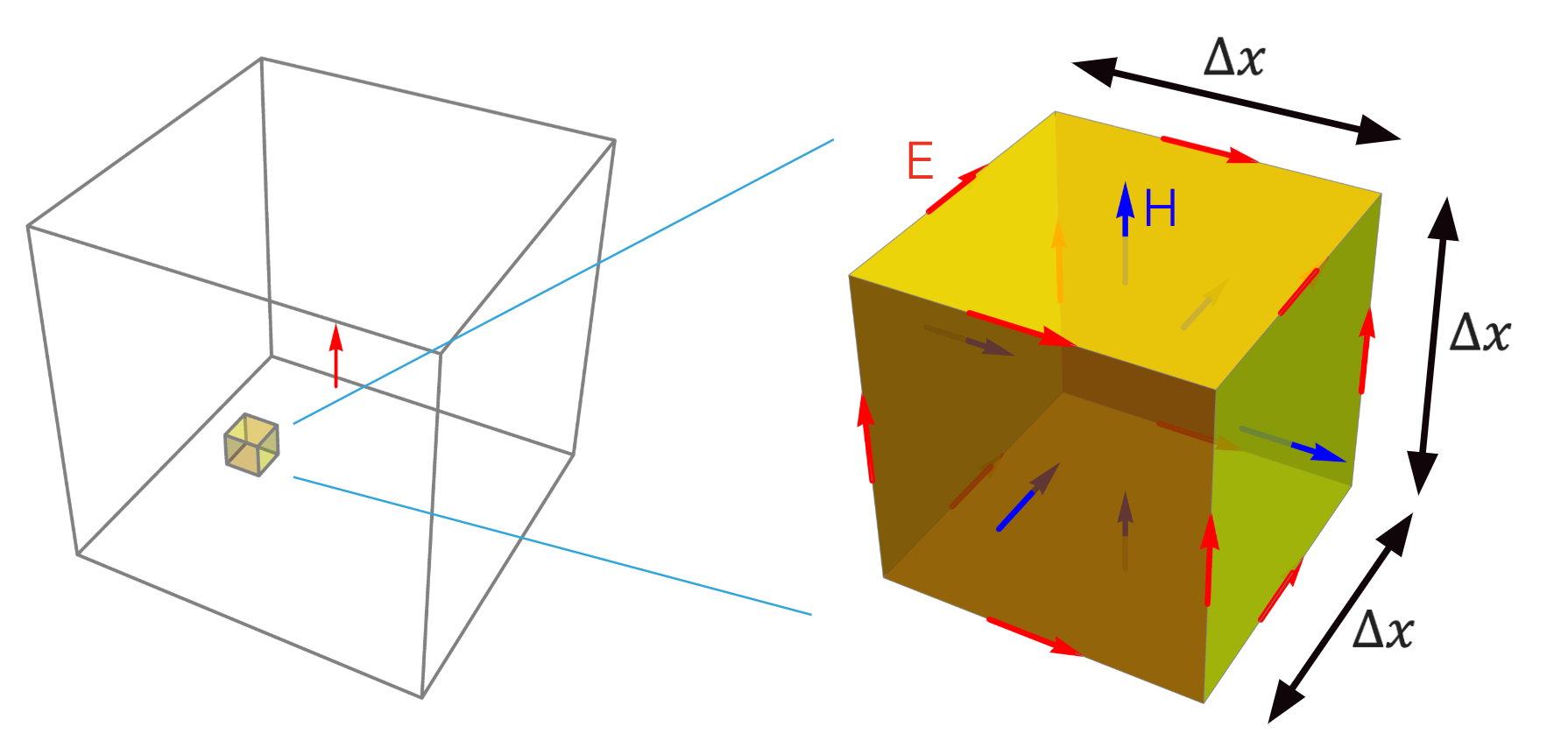
Note

A typical rule of thumb is to choose the discretization to be about \(\frac{\lambda_m}{20}\) where \(\lambda_m\) is the field wavelength.

Numerical Dispersion - 1D Illustration

Numerical dispersion is a form of numerical error dependent on the spatial and temporal discretization of the fields. In order to reduce it, it is necessary to improve the discretization of the simulation for particular frequencies and spatial features. This is an important aspect of defining the grid.

Consider a standard 1D wave equation in vacuum:

\[\left( \frac{\delta ^2 }{\delta x^2} - \frac{1}{c^2} \frac{\delta^2}{\delta t^2} \right) E = 0\]

which is ideally solved into a monochromatic travelling wave:

\[E(x) = e^{j (kx - \omega t)}\]

This physical wave is described with a wavevector \(k\) for the spatial field variations and the angular frequency \(\omega\) for temporal field variations. The spatial and temporal field variations are related by a dispersion relation.

The ideal dispersion relation is:

\[\left( \frac{\omega}{c} \right)^2 = k^2\]

However, in the FDTD simulation, the spatial and temporal fields are discrete.

../../_images/numerical_dispersion_grid_1d.png

The same 1D monochromatic wave can be solved using the FDTD method where \(m\) is the index in the grid:

\[\frac{\delta^2}{\delta x^2} E(x_i) \approx \frac{1}{\Delta x^2} \left[ E(x_i + \Delta x) + E(x_i - \Delta x) - 2 E(x_i) \right]\]

\[\frac{\delta^2}{\delta t^2} E(t_{\alpha}) \approx \frac{1}{\Delta t^2} \left[ E(t_{\alpha} + \Delta t) + E(t_{\alpha} - \Delta t) - 2 E(t_{\alpha}) \right]\]

Hence, these discrete fields have this new dispersion relation:

\[\left( \frac{1}{c \Delta t} \text{sin} \left( \frac{\omega \Delta t}{2} \right)^2 \right) = \left( \frac{1}{\Delta x} \text{sin} \left( \frac{k \Delta x}{2} \right) \right)^2\]

The ideal wave solution and the discrete solution have a mismatch illustrated below as a result of the numerical error introduced by numerical dispersion. This plot illustrates the angular frequency as a function of wavevector for both the physical ideal wave and the numerical discrete wave implemented in FDTD.

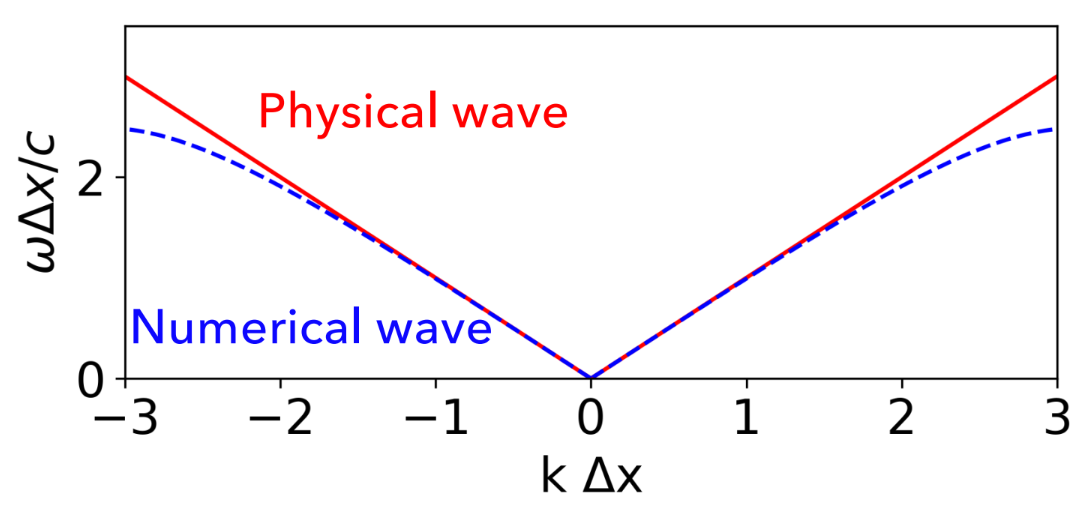
../../_images/numerical_dispersion_discretization_1d.png

At lower frequencies, when the discretization of \(\Delta x\) is small compared to the wavelength the error between the solutions is very low. When this proportionality increases between the spatial step size and the angular wavelength, this introduces numerical dispersion errors.

\[k \Delta x = \frac{2 \pi}{\lambda_k} \Delta x\]

Usage Recommendations

It is important to understand the relationship between the time-step \(\Delta t\) defined by the courant factor, and the spatial grid distribution to guarantee simulation stability.
If your structure has small features, consider using a spatially nonuniform grid. This guarantees finer spatial resolution near the features, but away from it you use have a larger (and computationally faster) grid. In this case, the time step \(\Delta t\) is defined by the smallest spatial grid size.

See also

courant

The Courant-Friedrichs-Lewy (CFL) stability factor

GridSpec

Collective grid specification for all three dimensions.

UniformGrid

Uniform 1D grid.

AutoGrid

Specification for non-uniform grid along a given dimension.

Notebooks:

Using automatic nonuniform meshing

Lectures:

shutoff#: Ratio of the instantaneous integrated E-field intensity to the maximum value at which the simulation will automatically terminate time stepping. Used to prevent extraneous run time of simulations with fully decayed fields. Set to 0 to disable this feature.

subpixel#

If True, uses subpixel averaging of the permittivity based on structure definition, resulting in much higher accuracy for a given grid size.,

1D Illustration

For example, in the image below, two silicon slabs with thicknesses 150nm and 175nm centered in a grid with spatial discretization \(\Delta z = 25\text{nm}\) compute the effective permittivity of each grid point as the average permittivity between the grid points. A simplified equation based on the ratio \(\eta\) between the permittivity of the two materials at the interface in this case:

\[\epsilon_{eff} = \eta \epsilon_{si} + (1 - \eta) \epsilon_{air}\]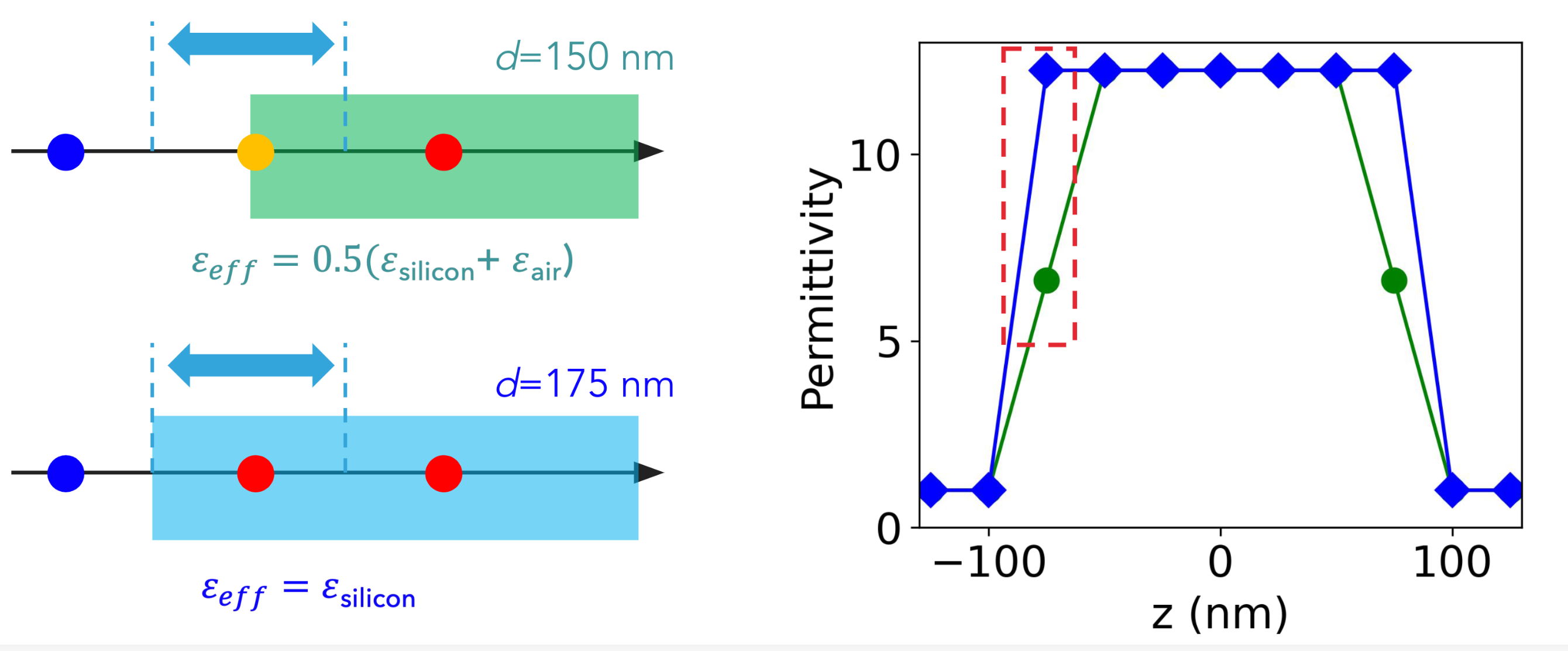

../../_images/subpixel_permittivity_1d.png

However, in this 1D case, this averaging is accurate because the dominant electric field is parallel to the dielectric grid points.

You can learn more about the subpixel averaging derivation from Maxwell’s equations in 1D in this lecture: Introduction to subpixel averaging.

2D & 3D Usage Caveats

In 2D, the subpixel averaging implementation depends on the polarization (\(s\) or \(p\)) of the incident electric field on the interface.
In 3D, the subpixel averaging is implemented with tensorial averaging due to arbitrary surface and field spatial orientations.

See also

Lectures:

normalize_index#: Index of the source in the tuple of sources whose spectrum will be used to normalize the frequency-dependent data. If None, the raw field data is returned. If None, the raw field data is returned unnormalized.

courant#

The Courant-Friedrichs-Lewy (CFL) stability factor \(C\), controls time step to spatial step ratio. A physical wave has to propagate slower than the numerical information propagation in a Yee-cell grid. This is because in this spatially-discrete grid, information propagates over 1 spatial step \(\Delta x\) over a time step \(\Delta t\). This constraint enables the correct physics to be captured by the simulation.

1D Illustration

In a 1D model:

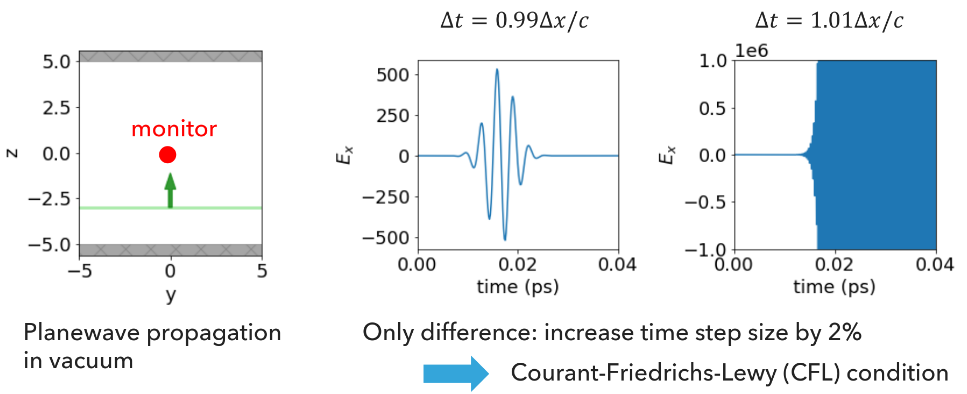
Lower values lead to more stable simulations for dispersive materials, but result in longer simulation times. This factor is normalized to no larger than 1 when CFL stability condition is met in 3D.

For a 1D grid:

\[C_{\text{1D}} = \frac{\Delta x}{c \Delta t} \leq 1\]

2D Illustration

In a 2D grid, where the \(E_z\) field is at the red dot center surrounded by four green magnetic edge components in a square Yee cell grid:

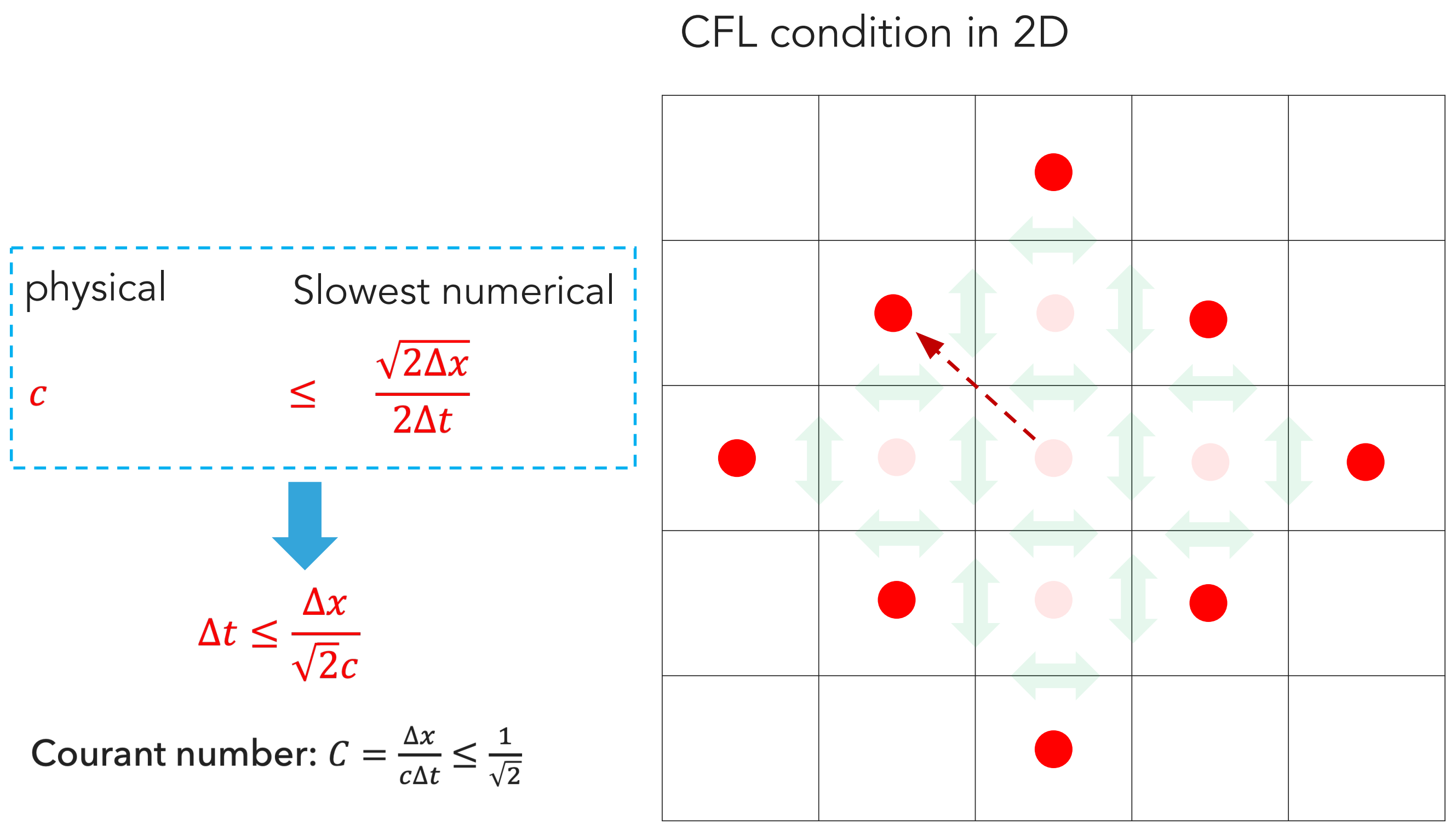../../_images/courant_instability_2d.png

\[C_{\text{2D}} = \frac{\Delta x}{c \Delta t} \leq \frac{1}{\sqrt{2}}\]

Hence, for the same spatial grid, the time step in 2D grid needs to be smaller than the time step in a 1D grid.

3D Illustration

For an isotropic medium with refractive index \(n\), the 3D time step condition can be derived to be:

\[\Delta t \le \frac{n}{c \sqrt{\frac{1}{\Delta x^2} + \frac{1}{\Delta y^2} + \frac{1}{\Delta z^2}}}\]

In this case, the number of spatial grid points scale by \(\sim \frac{1}{\Delta x^3}\) where \(\Delta x\) is the spatial discretization in the \(x\) dimension. If the total simulation time is kept the same whilst maintaining the CFL condition, then the number of time steps required scale by \(\sim \frac{1}{\Delta x}\). Hence, the spatial grid discretization influences the total time-steps required. The total simulation scaling per spatial grid size in this case is by \(\sim \frac{1}{\Delta x^4}.\)

As an example, in this case, refining the mesh by a factor or 2 (reducing the spatial step size by half) \(\Delta x \to \frac{\Delta x}{2}\) will increase the total simulation computational cost by 16.

Divergence Caveats

tidy3d uses a default Courant factor of 0.99. When a dispersive material with eps_inf < 1 is used, the Courant factor will be automatically adjusted to be smaller than sqrt(eps_inf) to ensure stability. If your simulation still diverges despite addressing any other issues discussed above, reducing the Courant factor may help.

See also

grid_spec

Specifications for the simulation grid along each of the three directions.

Lectures:

classmethod bloch_with_symmetry(val, values)[source]#: Error if a Bloch boundary is applied with symmetry

classmethod plane_wave_boundaries(val, values)[source]#: Error if there are plane wave sources incompatible with boundary conditions.

classmethod tfsf_boundaries(val, values)[source]#: Error if the boundary conditions are compatible with TFSF sources, if any.

classmethod tfsf_with_symmetry(val, values)[source]#: Error if a TFSF source is applied with symmetry

classmethod boundaries_for_zero_dims(val, values)[source]#: Error if absorbing boundaries, unmatching pec/pmc, or symmetry is used along a zero dimension.

classmethod diffraction_monitor_boundaries(val, values)[source]#: If any DiffractionMonitor exists, ensure boundary conditions in the transverse directions are periodic or Bloch.

classmethod proj_distance_for_approx(val, values)[source]#: Warn if projection distance for projection monitors is not large compared to monitor or, simulation size, yet far_field_approx is True.

classmethod diffraction_monitor_medium(val, values)[source]#: If any DiffractionMonitor exists, ensure is does not lie in a lossy medium.

validate_pre_upload(source_required=True)[source]#

Validate the fully initialized simulation is ok for upload to our servers.

Parameters:: source_required (bool = True) – If True, validation will fail in case no sources are found in the simulation.

property monitors_data_size#: Dictionary mapping monitor names to their estimated storage size in bytes.

property mediums#

Returns set of distinct AbstractMedium in simulation.

Returns:: Set of distinct mediums in the simulation.
Return type:: List[AbstractMedium]

property medium_map#

Returns dict mapping medium to index in material. medium_map[medium] returns unique global index of AbstractMedium in simulation.

Returns:: Mapping between distinct mediums to index in simulation.
Return type:: Dict[AbstractMedium, int]

property background_structure#: Returns structure representing the background of the Simulation.

static intersecting_media(test_object, structures)[source]#

From a given list of structures, returns a list of AbstractMedium associated with those structures that intersect with the test_object, if it is a surface, or its surfaces, if it is a volume.

Parameters:

test_object (Box) – Object for which intersecting media are to be detected.
structures (List[AbstractMedium]) – List of structures whose media will be tested.

Returns:

Set of distinct mediums that intersect with the given planar object.

Return type:

List[AbstractMedium]

static intersecting_structures(test_object, structures)[source]#

From a given list of structures, returns a list of Structure that intersect with the test_object, if it is a surface, or its surfaces, if it is a volume.

Parameters:

test_object (Box) – Object for which intersecting media are to be detected.
structures (List[AbstractMedium]) – List of structures whose media will be tested.

Returns:

Set of distinct structures that intersect with the given surface, or with the surfaces of the given volume.

Return type:

List[Structure]

monitor_medium(monitor)[source]#

Return the medium in which the given monitor resides.

Parameters:: monitor (Monitor) – Monitor whose associated medium is to be returned.
Returns:: Medium associated with the given Monitor.
Return type:: AbstractMedium

to_gdstk(x=None, y=None, z=None, permittivity_threshold=1, frequency=0, gds_layer_dtype_map=None)[source]#

Convert a simulation’s planar slice to a .gds type polygon list.

Parameters:

x (float = None) – Position of plane in x direction, only one of x,y,z can be specified to define plane.
y (float = None) – Position of plane in y direction, only one of x,y,z can be specified to define plane.
z (float = None) – Position of plane in z direction, only one of x,y,z can be specified to define plane.
permittivity_threshold (float = 1.001) – Permitivitty value used to define the shape boundaries for structures with custom medim
frequency (float = 0) – Frequency for permittivity evaluaiton in case of custom medium (Hz).
gds_layer_dtype_map (Dict) – Dictionary mapping mediums to GDSII layer and data type tuples.

Returns:

List of gdstk.Polygon.

Return type:

List

to_gdspy(x=None, y=None, z=None, gds_layer_dtype_map=None)[source]#

Convert a simulation’s planar slice to a .gds type polygon list.

Parameters:

x (float = None) – Position of plane in x direction, only one of x,y,z can be specified to define plane.
y (float = None) – Position of plane in y direction, only one of x,y,z can be specified to define plane.
z (float = None) – Position of plane in z direction, only one of x,y,z can be specified to define plane.
gds_layer_dtype_map (Dict) – Dictionary mapping mediums to GDSII layer and data type tuples.

Returns:

List of gdspy.Polygon and gdspy.PolygonSet.

Return type:

List

to_gds(cell, x=None, y=None, z=None, permittivity_threshold=1, frequency=0, gds_layer_dtype_map=None)[source]#

Append the simulation structures to a .gds cell.

Parameters:

cell (gdstk.Cell or gdspy.Cell) – Cell object to which the generated polygons are added.
x (float = None) – Position of plane in x direction, only one of x,y,z can be specified to define plane.
y (float = None) – Position of plane in y direction, only one of x,y,z can be specified to define plane.
z (float = None) – Position of plane in z direction, only one of x,y,z can be specified to define plane.
permittivity_threshold (float = 1.001) – Permitivitty value used to define the shape boundaries for structures with custom medim
frequency (float = 0) – Frequency for permittivity evaluaiton in case of custom medium (Hz).
gds_layer_dtype_map (Dict) – Dictionary mapping mediums to GDSII layer and data type tuples.

to_gds_file(fname, x=None, y=None, z=None, permittivity_threshold=1, frequency=0, gds_layer_dtype_map=None, gds_cell_name='MAIN')[source]#

Append the simulation structures to a .gds cell.

Parameters:

fname (str) – Full path to the .gds file to save the Simulation slice to.
x (float = None) – Position of plane in x direction, only one of x,y,z can be specified to define plane.
y (float = None) – Position of plane in y direction, only one of x,y,z can be specified to define plane.
z (float = None) – Position of plane in z direction, only one of x,y,z can be specified to define plane.
permittivity_threshold (float = 1.001) – Permitivitty value used to define the shape boundaries for structures with custom medim
frequency (float = 0) – Frequency for permittivity evaluaiton in case of custom medium (Hz).
gds_layer_dtype_map (Dict) – Dictionary mapping mediums to GDSII layer and data type tuples.
gds_cell_name (str = 'MAIN') – Name of the cell created in the .gds file to store the geometry.

plot(x=None, y=None, z=None, ax=None, source_alpha=None, monitor_alpha=None, hlim=None, vlim=None, **patch_kwargs)[source]#

Plot each of simulation’s components on a plane defined by one nonzero x,y,z coordinate.

Parameters:

x (float = None) – position of plane in x direction, only one of x, y, z must be specified to define plane.
y (float = None) – position of plane in y direction, only one of x, y, z must be specified to define plane.
z (float = None) – position of plane in z direction, only one of x, y, z must be specified to define plane.
source_alpha (float = None) – Opacity of the sources. If None, uses Tidy3d default.
monitor_alpha (float = None) – Opacity of the monitors. If None, uses Tidy3d default.
ax (matplotlib.axes._subplots.Axes = None) – Matplotlib axes to plot on, if not specified, one is created.
hlim (Tuple[float, float] = None) – The x range if plotting on xy or xz planes, y range if plotting on yz plane.
vlim (Tuple[float, float] = None) – The z range if plotting on xz or yz planes, y plane if plotting on xy plane.

Returns:

The supplied or created matplotlib axes.

Return type:

matplotlib.axes._subplots.Axes

See also

Notebooks

Visualizing geometries in Tidy3D: Plotting Materials

plot_eps(x=None, y=None, z=None, freq=None, alpha=None, source_alpha=None, monitor_alpha=None, hlim=None, vlim=None, ax=None)[source]#

Plot each of simulation’s components on a plane defined by one nonzero x,y,z coordinate. The permittivity is plotted in grayscale based on its value at the specified frequency.

Parameters:

x (float = None) – position of plane in x direction, only one of x, y, z must be specified to define plane.
y (float = None) – position of plane in y direction, only one of x, y, z must be specified to define plane.
z (float = None) – position of plane in z direction, only one of x, y, z must be specified to define plane.
freq (float = None) – Frequency to evaluate the relative permittivity of all mediums. If not specified, evaluates at infinite frequency.
alpha (float = None) – Opacity of the structures being plotted. Defaults to the structure default alpha.
source_alpha (float = None) – Opacity of the sources. If None, uses Tidy3d default.
monitor_alpha (float = None) – Opacity of the monitors. If None, uses Tidy3d default.
ax (matplotlib.axes._subplots.Axes = None) – Matplotlib axes to plot on, if not specified, one is created.
hlim (Tuple[float, float] = None) – The x range if plotting on xy or xz planes, y range if plotting on yz plane.
vlim (Tuple[float, float] = None) – The z range if plotting on xz or yz planes, y plane if plotting on xy plane.

Returns:

The supplied or created matplotlib axes.

Return type:

matplotlib.axes._subplots.Axes

See also

Notebooks

Visualizing geometries in Tidy3D: Plotting Permittivity

plot_structures_eps(x=None, y=None, z=None, freq=None, alpha=None, cbar=True, reverse=False, ax=None, hlim=None, vlim=None)[source]#

Plot each of simulation’s structures on a plane defined by one nonzero x,y,z coordinate. The permittivity is plotted in grayscale based on its value at the specified frequency.

Parameters:

x (float = None) – position of plane in x direction, only one of x, y, z must be specified to define plane.
y (float = None) – position of plane in y direction, only one of x, y, z must be specified to define plane.
z (float = None) – position of plane in z direction, only one of x, y, z must be specified to define plane.
freq (float = None) – Frequency to evaluate the relative permittivity of all mediums. If not specified, evaluates at infinite frequency.
reverse (bool = False) – If False, the highest permittivity is plotted in black. If True, it is plotteed in white (suitable for black backgrounds).
cbar (bool = True) – Whether to plot a colorbar for the relative permittivity.
alpha (float = None) – Opacity of the structures being plotted. Defaults to the structure default alpha.
ax (matplotlib.axes._subplots.Axes = None) – Matplotlib axes to plot on, if not specified, one is created.
hlim (Tuple[float, float] = None) – The x range if plotting on xy or xz planes, y range if plotting on yz plane.
vlim (Tuple[float, float] = None) – The z range if plotting on xz or yz planes, y plane if plotting on xy plane.

Returns:

The supplied or created matplotlib axes.

Return type:

matplotlib.axes._subplots.Axes

eps_bounds(freq=None)[source]#: Compute range of (real) permittivity present in the simulation at frequency “freq”.

property num_pml_layers#

Number of absorbing layers in all three axes and directions (-, +).

Returns:: List containing the number of absorber layers in - and + boundaries.
Return type:: List[Tuple[float, float]]

property pml_thicknesses#

Thicknesses (um) of absorbers in all three axes and directions (-, +)

Returns:: List containing the absorber thickness (micron) in - and + boundaries.
Return type:: List[Tuple[float, float]]

property bounds_pml#: Simulation bounds including the PML regions.

property simulation_bounds#: Simulation bounds including the PML regions.

plot_pml(x=None, y=None, z=None, hlim=None, vlim=None, ax=None)[source]#

Plot each of simulation’s absorbing boundaries on a plane defined by one nonzero x,y,z coordinate.

Parameters:

x (float = None) – position of plane in x direction, only one of x, y, z must be specified to define plane.
y (float = None) – position of plane in y direction, only one of x, y, z must be specified to define plane.
z (float = None) – position of plane in z direction, only one of x, y, z must be specified to define plane
hlim (Tuple[float, float] = None) – The x range if plotting on xy or xz planes, y range if plotting on yz plane.
vlim (Tuple[float, float] = None) – The z range if plotting on xz or yz planes, y plane if plotting on xy plane.
ax (matplotlib.axes._subplots.Axes = None) – Matplotlib axes to plot on, if not specified, one is created.

Returns:

The supplied or created matplotlib axes.

Return type:

matplotlib.axes._subplots.Axes

plot_grid(x=None, y=None, z=None, ax=None, hlim=None, vlim=None, **kwargs)[source]#

Plot the cell boundaries as lines on a plane defined by one nonzero x,y,z coordinate.

Parameters:

x (float = None) – position of plane in x direction, only one of x, y, z must be specified to define plane.
y (float = None) – position of plane in y direction, only one of x, y, z must be specified to define plane.
z (float = None) – position of plane in z direction, only one of x, y, z must be specified to define plane.
hlim (Tuple[float, float] = None) – The x range if plotting on xy or xz planes, y range if plotting on yz plane.
vlim (Tuple[float, float] = None) – The z range if plotting on xz or yz planes, y plane if plotting on xy plane.
ax (matplotlib.axes._subplots.Axes = None) – Matplotlib axes to plot on, if not specified, one is created.
**kwargs – Optional keyword arguments passed to the matplotlib LineCollection. For details on accepted values, refer to Matplotlib’s documentation.

Returns:

The supplied or created matplotlib axes.

Return type:

matplotlib.axes._subplots.Axes

plot_boundaries(x=None, y=None, z=None, ax=None, **kwargs)[source]#

Plot the simulation boundary conditions as lines on a plane: defined by one nonzero x,y,z coordinate.

Parameters:

x (float = None) – position of plane in x direction, only one of x, y, z must be specified to define plane.
y (float = None) – position of plane in y direction, only one of x, y, z must be specified to define plane.
z (float = None) – position of plane in z direction, only one of x, y, z must be specified to define plane.
ax (matplotlib.axes._subplots.Axes = None) – Matplotlib axes to plot on, if not specified, one is created.
**kwargs –
Optional keyword arguments passed to the matplotlib LineCollection. For details on accepted values, refer to Matplotlib’s documentation.

Returns:

The supplied or created matplotlib axes.

Return type:

matplotlib.axes._subplots.Axes

property frequency_range#

Range of frequencies spanning all sources’ frequency dependence.

Returns:: Minimum and maximum frequencies of the power spectrum of the sources.
Return type:: Tuple[float, float]

plot_3d(width=800, height=800)[source]#: Render 3D plot of Simulation (in jupyter notebook only). :param width: width of the 3d view dom’s size :type width: float = 800 :param height: height of the 3d view dom’s size :type height: float = 800

property dt#

Simulation time step (distance).

Returns:: Time step (seconds).
Return type:: float

property tmesh#

FDTD time stepping points.

Returns:: Times (seconds) that the simulation time steps through.
Return type:: np.ndarray

property num_time_steps#: Number of time steps in simulation.

property grid#

FDTD grid spatial locations and information.

Returns:: Grid storing the spatial locations relevant to the simulation.
Return type:: Grid

property num_cells#

Number of cells in the simulation.

Returns:: Number of yee cells in the simulation.
Return type:: int

property wvl_mat_min#

Minimum wavelength in the material.

Returns:: Minimum wavelength in the material (microns).
Return type:: float

property complex_fields#

Whether complex fields are used in the simulation. Currently this only happens when there are Bloch boundaries.

Returns:: Whether the time-stepping fields are real or complex.
Return type:: bool

property nyquist_step#

Maximum number of discrete time steps to keep sampling below Nyquist limit.

Returns:: The largest N such that N * self.dt is below the Nyquist limit.
Return type:: int

discretize_monitor(monitor)[source]#: Grid on which monitor data corresponding to a given monitor will be computed.

discretize(box, extend=False)[source]#

Grid containing only cells that intersect with a Box.

Parameters:

box (Box) – Rectangular geometry within simulation to discretize.
extend (bool = False) – If True, ensure that the returned indexes extend sufficiently in every direction to be able to interpolate any field component at any point within the box, for field components sampled on the Yee grid.

Returns:

The FDTD subgrid containing simulation points that intersect with box.

Return type:

Grid

__hash__()#: Hash method.

epsilon(box, coord_key='centers', freq=None)[source]#

Get array of permittivity at volume specified by box and freq.

Parameters:

box (Box) – Rectangular geometry specifying where to measure the permittivity.
coord_key (str = 'centers') – Specifies at what part of the grid to return the permittivity at. Accepted values are {'centers', 'boundaries', 'Ex', 'Ey', 'Ez', 'Exy', 'Exz', 'Eyx', 'Eyz', 'Ezx', Ezy'}. The field values (eg. ‘Ex’) correspond to the corresponding field locations on the yee lattice. If field values are selected, the corresponding diagonal (eg. eps_xx in case of Ex) or off-diagonal (eg. eps_xy in case of Exy) epsilon component from the epsilon tensor is returned. Otherwise, the average of the main values is returned.
freq (float = None) – The frequency to evaluate the mediums at. If not specified, evaluates at infinite frequency.

Returns:

Datastructure containing the relative permittivity values and location coordinates. For details on xarray DataArray objects, refer to xarray’s Documentation.

Return type:

xarray.DataArray

See also

Notebooks

First walkthrough: permittivity data

epsilon_on_grid(grid, coord_key='centers', freq=None)[source]#

Get array of permittivity at a given freq on a given grid.

Parameters:

grid (Grid) – Grid specifying where to measure the permittivity.
coord_key (str = 'centers') – Specifies at what part of the grid to return the permittivity at. Accepted values are {'centers', 'boundaries', 'Ex', 'Ey', 'Ez', 'Exy', 'Exz', 'Eyx', 'Eyz', 'Ezx', Ezy'}. The field values (eg. ‘Ex’) correspond to the corresponding field locations on the yee lattice. If field values are selected, the corresponding diagonal (eg. eps_xx in case of Ex) or off-diagonal (eg. eps_xy in case of Exy) epsilon component from the epsilon tensor is returned. Otherwise, the average of the main values is returned.
freq (float = None) – The frequency to evaluate the mediums at. If not specified, evaluates at infinite frequency.

Returns:

Datastructure containing the relative permittivity values and location coordinates. For details on xarray DataArray objects, refer to xarray’s Documentation.

Return type:

xarray.DataArray

property custom_datasets#: List of custom datasets for verification purposes. If the list is not empty, then the simulation needs to be exported to hdf5 to store the data.

property volumetric_structures#: Generate a tuple of structures wherein any 2D materials are converted to 3D volumetric equivalents.

property allow_gain#: True if any of the mediums in the simulation allows gain.

perturbed_mediums_copy(temperature=None, electron_density=None, hole_density=None, interp_method='linear')[source]#

Return a copy of the simulation with heat and/or charge data applied to all mediums that have perturbation models specified. That is, such mediums will be replaced with spatially dependent custom mediums that reflect perturbation effects. Any of temperature, electron_density, and hole_density can be None. All provided fields must have identical coords.

Parameters:

temperature (SpatialDataArray = None) – Temperature field data.
electron_density (SpatialDataArray = None) – Electron density field data.
hole_density (SpatialDataArray = None) – Hole density field data.
interp_method (InterpMethod, optional) – Interpolation method to obtain heat and/or charge values that are not supplied at the Yee grids.

Returns:

Simulation after application of heat and/or charge data.

Return type:

Simulation

classmethod from_scene(scene, **kwargs)[source]#

Create a simulation from a Scene instance. Must provide additional parameters to define a valid simulation (for example, run_time, grid_spec, etc).

Parameters:

scene (Scene) – Size of object in x, y, and z directions.
**kwargs – Other arguments passed to new simulation instance.

Example

>>> from tidy3d import Scene, Medium, Box, Structure, GridSpec
>>> box = Structure(
...     geometry=Box(center=(0, 0, 0), size=(1, 2, 3)),
...     medium=Medium(permittivity=5),
... )
>>> scene = Scene(
...     structures=[box],
...     medium=Medium(permittivity=3),
... )
>>> sim = Simulation.from_scene(
...     scene=scene,
...     center=(0, 0, 0),
...     size=(5, 6, 7),
...     run_time=1e-12,
...     grid_spec=GridSpec.uniform(dl=0.4),
... )

subsection(region, boundary_spec=None, grid_spec=None, symmetry=None, sources=None, monitors=None, remove_outside_structures=True, remove_outside_custom_mediums=False, **kwargs)[source]#

Generate a simulation instance containing only the region.

Parameters:

region (:class:.`Box`) – New simulation domain.
boundary_spec (:class:.`BoundarySpec` = None) – New boundary specification. If None, then it is inherited from the original simulation.
grid_spec (:class:.`GridSpec` = None) – New grid specification. If None, then it is inherited from the original simulation. If identical, then the original grid is transferred directly as a :class:.`CustomGrid`. Note that in the latter case the region of the new simulation is snapped to the original grid lines.
symmetry (Tuple[Literal[0, -1, 1], Literal[0, -1, 1], Literal[0, -1, 1]] = None) – New simulation symmetry. If None, then it is inherited from the original simulation. Note that in this case the size and placement of new simulation domain must be commensurate with the original symmetry.
sources (Tuple[SourceType, ...] = None) – New list of sources. If None, then the sources intersecting the new simulation domain are inherited from the original simulation.
monitors (Tuple[MonitorType, ...] = None) – New list of monitors. If None, then the monitors intersecting the new simulation domain are inherited from the original simulation.
remove_outside_structures (bool = True) – Remove structures outside of the new simulation domain.
remove_outside_custom_mediums (bool = True) – Remove custom medium data outside of the new simulation domain.
**kwargs – Other arguments passed to new simulation instance.

`Type`	Tuple[float, float, float]
`Default`	= (0.0, 0.0, 0.0)
`Units`	um
`Description`	Center of object in x, y, and z.

`Type`	Tuple[NonNegativeFloat, NonNegativeFloat, NonNegativeFloat]
`Default`
`Units`	um
`Description`	Size in x, y, and z directions.

`Type`	str
`Default`	= 2.6.0rc1
`Description`	String specifying the front end version number.

`Type`	bool
`Default`	= True
`Description`	If `True`, uses subpixel averaging of the permittivity based on structure definition, resulting in much higher accuracy for a given grid size.

tidy3d.Simulation

Contents

tidy3d.Simulation#