tidy3d.FieldProjectionCartesianMonitor

class FieldProjectionCartesianMonitor

Bases: AbstractFieldProjectionMonitor

Monitor that samples electromagnetic near fields in the frequency domain and projects them on a Cartesian observation plane.

Parameters:

• center (Attribute: center) –

  Type	Tuple[float, float, float]
  Default	= (0.0, 0.0, 0.0)
  Units	um
  Description	Center of object in x, y, and z.

• size (Attribute: size) –

  Type	Tuple[NonNegativeFloat, NonNegativeFloat, NonNegativeFloat]
  Default
  Units	um
  Description	Size in x, y, and z directions.

• name (Attribute: name) –

  Type	ConstrainedStrValue
  Default
  Description	Unique name for monitor.

• interval_space (Attribute: interval_space) –

  Type	Tuple[PositiveInt, PositiveInt, PositiveInt]
  Default	= (1, 1, 1)
  Description	Number of grid step intervals at which near fields are recorded for projection to the far field, along each direction. If equal to 1, there will be no downsampling. If greater than 1, the step will be applied, but the first and last point of the monitor grid are always included. Using values greater than 1 can help speed up server-side far field projections with minimal accuracy loss, especially in cases where it is necessary for the grid resolution to be high for the FDTD simulation, but such a high resolution is unnecessary for the purpose of projecting the recorded near fields to the far field.

• colocate (Attribute: colocate) –

  Type	Literal[True]
  Default	= True
  Description	Defines whether fields are colocated to grid cell boundaries (i.e. to the primal grid) on-the-fly during a solver run. Can be toggled for field recording monitors and is hard-coded for other monitors depending on their specific function.

• freqs (Attribute: freqs) –

  Type	Union[Tuple[float, …], ArrayLike[dtype=float, ndim=1]]
  Default
  Units	Hz
  Description	Array or list of frequencies stored by the field monitor.

• apodization (Attribute: apodization) –

  Type	ApodizationSpec
  Default	= ApodizationSpec(startNone, endNone, widthNone, type’ApodizationSpec’)
  Description	Sets parameters of (optional) apodization. Apodization applies a windowing function to the Fourier transform of the time-domain fields into frequency-domain ones, and can be used to truncate the beginning and/or end of the time signal, for example to eliminate the source pulse when studying the eigenmodes of a system. Note: apodization affects the normalization of the frequency-domain fields.

• normal_dir (Attribute: normal_dir) –

  Type	Optional[Literal[‘+’, ‘-‘]]
  Default	= None
  Description	Direction of the surface monitor’s normal vector w.r.t. the positive x, y or z unit vectors. Must be one of '+' or '-'. Applies to surface monitors only, and defaults to '+' if not provided.

• exclude_surfaces (Attribute: exclude_surfaces) –

  Type	Optional[Tuple[Literal[‘x-’, ‘x+’, ‘y-’, ‘y+’, ‘z-’, ‘z+’], …]]
  Default	= None
  Description	Surfaces to exclude in the integration, if a volume monitor.

• custom_origin (Attribute: custom_origin) –

  Type	Optional[Tuple[float, float, float]]
  Default	= None
  Units	um
  Description	Local origin used for defining observation points. If None, uses the monitor’s center.

• far_field_approx (Attribute: far_field_approx) –

  Type	bool
  Default	= True
  Description	Whether to enable the far field approximation when projecting fields. If True, terms that decay as O(1/r^2) are ignored, as are the radial components of fields. Typically, this should be set to True only when the projection distance is much larger than the size of the device being modeled, and the projected points are in the far field of the device.

• window_size (Attribute: window_size) –

  Type	Tuple[NonNegativeFloat, NonNegativeFloat]
  Default	= (0, 0)
  Description	Size of the transition region of the windowing function used to ensure that the recorded near fields decay to zero near the edges of the monitor. The two components refer to the two tangential directions associated with each surface. For surfaces with the normal along x, the two components are (y, z). For surfaces with the normal along y, the two components are (x, z). For surfaces with the normal along z, the two components are (x, y). Each value must be between 0 and 1, inclusive, and denotes the size of the transition region over which fields are scaled to less than a thousandth of the original amplitude, relative to half the size of the monitor in that direction. A value of 0 turns windowing off in that direction, while a value of 1 indicates that the window will be applied to the entire monitor in that direction. This field is applicable for surface monitors only, and otherwise must remain (0, 0).

• medium (Attribute: medium) –

  Type	Union[Medium, AnisotropicMedium, PECMedium, PoleResidue, Sellmeier, Lorentz, Debye, Drude, FullyAnisotropicMedium, CustomMedium, CustomPoleResidue, CustomSellmeier, CustomLorentz, CustomDebye, CustomDrude, CustomAnisotropicMedium, PerturbationMedium, PerturbationPoleResidue, Medium2D]
  Default	= None
  Description	Medium through which to project fields. Generally, the fields should be projected through the same medium as the one in which this monitor is placed, and this is the default behavior when medium=None. A custom medium can be useful in some situations for advanced users, but we recommend trying to avoid using a non-default medium.

• proj_axis (Attribute: proj_axis) –

  Type	Literal[0, 1, 2]
  Default
  Description	Axis along which the observation plane is oriented.

• proj_distance (Attribute: proj_distance) –

  Type	float
  Default	= 1000000.0
  Units	um
  Description	Signed distance of the projection plane along proj_axis. from the plane containing local_origin.

• x (Attribute: x) –

  Type	Union[Tuple[float, …], ArrayLike[dtype=float, ndim=1]]
  Default
  Units	um
  Description	Local x observation coordinates w.r.t. local_origin and proj_axis. When proj_axis is 0, this corresponds to the global y axis. When proj_axis is 1, this corresponds to the global x axis. When proj_axis is 2, this corresponds to the global x axis.

• y (Attribute: y) –

  Type	Union[Tuple[float, …], ArrayLike[dtype=float, ndim=1]]
  Default
  Units	um
  Description	Local y observation coordinates w.r.t. local_origin and proj_axis. When proj_axis is 0, this corresponds to the global z axis. When proj_axis is 1, this corresponds to the global z axis. When proj_axis is 2, this corresponds to the global y axis.

Notes

Parameters Caveats

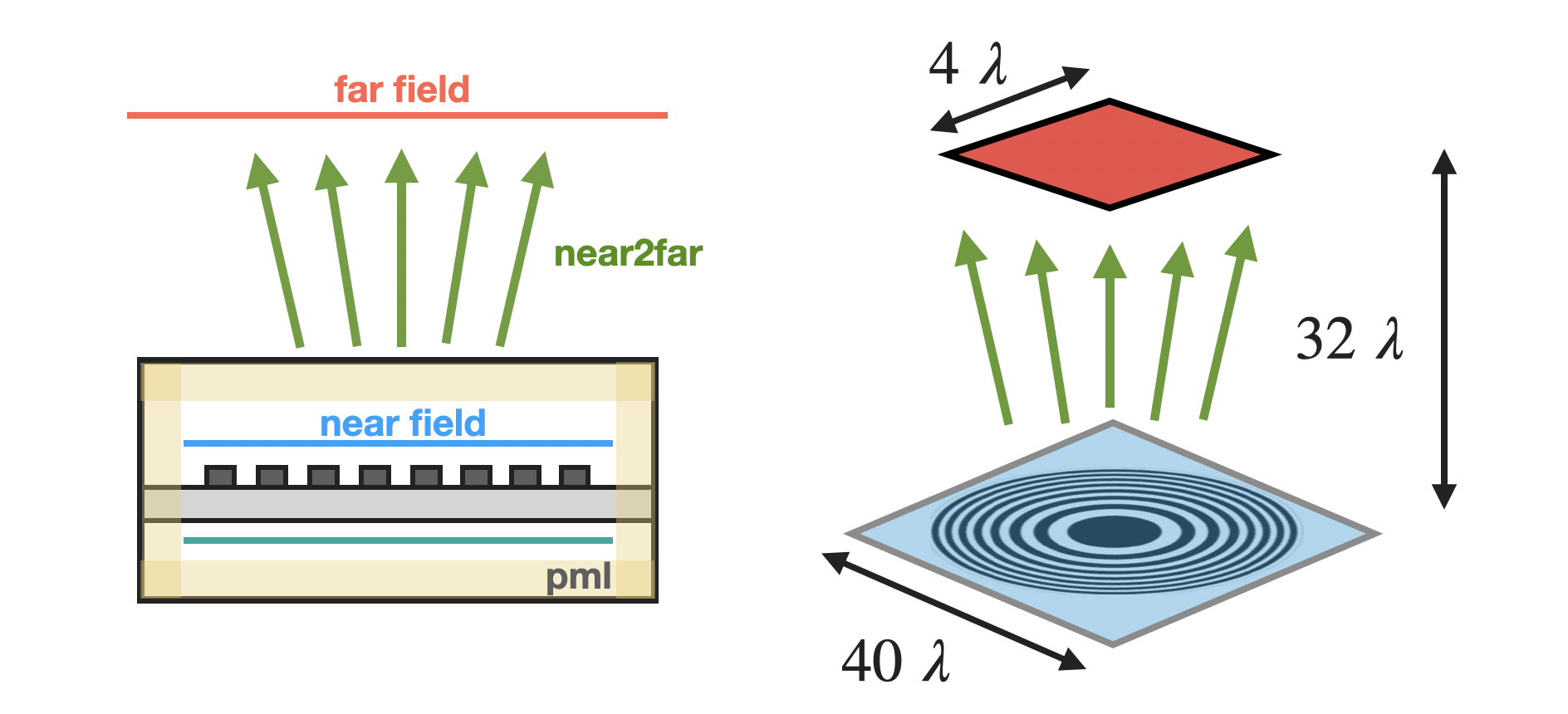
The center and size fields define where the monitor will be placed in order to record near fields, typically very close to the structure of interest. The near fields are then projected to far-field locations defined by x, y, and proj_distance, relative to the custom_origin.

Here, x and y, correspond to a local coordinate system where the local z axis is defined by proj_axis: which is the axis normal to this monitor.

Far-Field Approximation Selection

If the distance between the near and far field locations is much larger than the size of the device, one can typically set far_field_approx to True, which will make use of the far-field approximation to speed up calculations. If the projection distance is comparable to the size of the device, we recommend setting far_field_approx to False, so that the approximations are not used, and the projection is accurate even just a few wavelengths away from the near field locations.

For applications where the monitor is an open surface rather than a box that encloses the device, it is advisable to pick the size of the monitor such that the recorded near fields decay to negligible values near the edges of the monitor.

When selected, it is assumed that:

• The fields are measured at a distance much greater than the size of our simulation in the transverse direction.

• The geometric approximations imply that any quantity whose magnitude drops off as \(\frac{1}{r^2}\) or faster is ignored.

The advantages of these approximations are:

• The projections are computed relatively fast.

• The projections are cast in a simple mathematical form. which allows re-projecting the fields to different distance without the need to re-run a simulation or to re-run the FieldProjector.

  In cases where we may want to project to intermediate distances where the far field approximation is no longer valid, simply include the class definition parameter far_field_approx=False in the FieldProjectionCartesianMonitor instantiation. The resulting computations will be a bit slower, but the results will be significantly more accurate.

  Usage Caveats

  Since field projections rely on the surface equivalence principle, we have assumed that the tangential near fields recorded on the near field monitor serve as equivalent sources which generate the correct far fields. However, this requires that the field strength decays nearly to zero near the edges of the near-field monitor, which may not always be the case. For example, if we had used a larger aperture compared to the full simulation size in the transverse direction, we may expect a degradation in accuracy of the field projections. Despite this limitation, the field projections are still remarkably accurate in realistic scenarios. For realistic case studies further demonstrating the accuracy of the field projections, see our metalens and zone plate case studies.

  The field projections make use of the analytical homogeneous medium Green’s function, which assumes that the fields are propagating in a homogeneous medium. Therefore, one should use PMLs / absorbers as boundary conditions in the part of the domain where fields are projected. For far field projections in the context of perdiodic boundary conditions, see the diffraction efficiency example which demonstrates the use of a DiffractionMonitor.

  Server-side field projections will add to the monetary cost of the simulation. However, typically the far field projections have a very small computation cost compared to the FDTD simulation itself, so the increase in monetary cost should be negligibly small in most cases.

Example

>>> monitor = FieldProjectionCartesianMonitor(
...     center=(1,2,3),
...     size=(2,2,2),
...     freqs=[250e12, 300e12],
...     name='n2f_monitor',
...     custom_origin=(1,2,3),
...     x=[-1, 0, 1],
...     y=[-2, -1, 0, 1, 2],
...     proj_axis=2,
...     proj_distance=5,
...     far_field_approx=True,
...     )

See also

Notebooks:

• Performing near field to far field projections

• Field projection for a zone plate

• Metalens in the visible frequency range

• Multilevel blazed diffraction grating

Attributes

Methods

storage_size(num_cells, tmesh)

Size of monitor storage given the number of points after discretization.

proj_axis

proj_distance

x

y

storage_size(num_cells, tmesh)

Size of monitor storage given the number of points after discretization.

__hash__()

Hash method.