tidy3d.ModeSpec

class ModeSpec

Bases: Tidy3dBaseModel

Stores specifications for the mode solver to find an electromagntic mode.

Parameters:

• num_modes (PositiveInt = 1) – Number of modes returned by mode solver.

• target_neff (Optional[PositiveFloat] = None) – Guess for effective index of the mode.

• num_pml (Tuple[NonNegativeInt, NonNegativeInt] = (0, 0)) – Number of standard pml layers to add in the two tangential axes.

• filter_pol (Optional[Literal['te', 'tm']] = None) – The solver always computes the num_modes modes closest to the given target_neff. If filter_pol==None, they are simply sorted in order of decreasing effective index. If a polarization filter is selected, the modes are rearranged such that the first n_pol modes in the list are the ones with the selected polarization fraction larger than or equal to 0.5, while the next num_modes - n_pol modes are the ones where it is smaller than 0.5 (i.e. the opposite polarization fraction is larger than 0.5). Within each polarization subset, the modes are still ordered by decreasing effective index. te-fraction is defined as the integrated intensity of the E-field component parallel to the first plane axis, normalized to the total in-plane E-field intensity. Conversely, tm-fraction uses the E field component parallel to the second plane axis.

• angle_theta (float = 0.0) – [units = rad]. Polar angle of the propagation axis from the injection axis.

• angle_phi (float = 0.0) – [units = rad]. Azimuth angle of the propagation axis in the plane orthogonal to the injection axis.

• precision (Literal['single', 'double'] = single) – The solver will be faster and using less memory under single precision, but more accurate under double precision.

• bend_radius (Optional[float] = None) – [units = um]. A curvature radius for simulation of waveguide bends. Can be negative, in which case the mode plane center has a smaller value than the curvature center along the tangential axis perpendicular to the bend axis.

• bend_axis (Optional[Literal[0, 1]] = None) – Index into the two tangential axes defining the normal to the plane in which the bend lies. This must be provided if bend_radius is not None. For example, for a ring in the global xy-plane, and a mode plane in either the xz or the yz plane, the bend_axis is always 1 (the global z axis).

• track_freq (Optional[Literal['central', 'lowest', 'highest']] = central) – Parameter that turns on/off mode tracking based on their similarity. Can take values 'lowest', 'central', or 'highest', which correspond to mode tracking based on the lowest, central, or highest frequency. If None no mode tracking is performed.

• group_index_step (Union[PositiveFloat, bool] = False) – Control the computation of the group index alongside the effective index. If set to a positive value, it sets the fractional frequency step used in the numerical differentiation of the effective index to compute the group index. If set to True, the default of 0.005 is used.

Notes

The angle_theta and angle_phi parameters define the injection axis as illustrated in the figure below, with respect to the axis normal to the mode plane (x in the figure). Note that angle_theta must be smaller than \(\frac{pi}{2}\). To inject in the backward direction, we can still use the direction parameter as also shown in the figure. Similarly, the mode amplitudes computed in mode monitors are defined w.r.t. the forward and backward directions as illustrated. Note, the planar axes are found by popping the injection axis from {x,y,z}. For example, if injection axis is y, the planar axes are ordered {x,z}.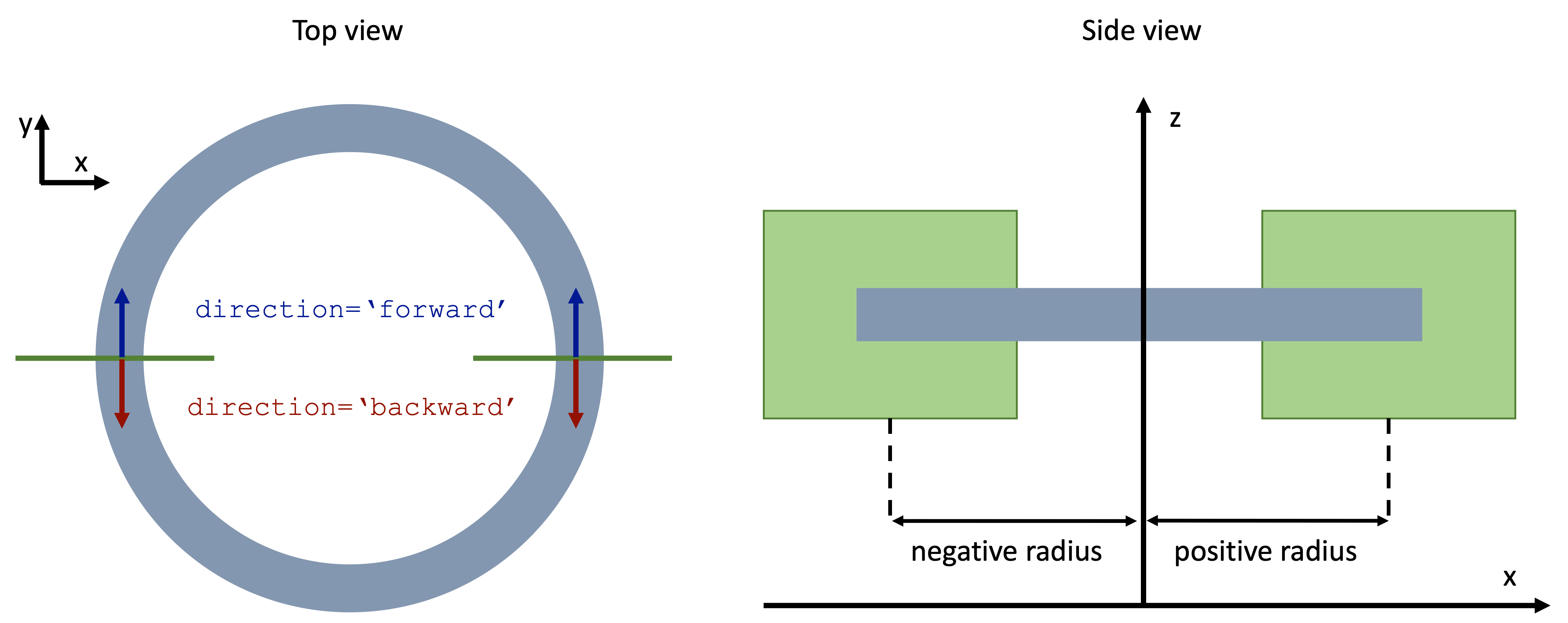

The bend_axis is the axis normal to the plane in which the bend lies, (z in the diagram below). In the mode specification, it is defined locally for the mode plane as one of the two axes tangential to the plane. In the case of bends that lie in the xy-plane, the mode plane would be either in xz or in yz, so in both cases the correct setting is bend_axis=1, selecting the global z. The bend_radius is counted from the center of the mode plane to the center of the curvature, along the tangential axis perpendicular to the bend axis. This radius can also be negative, if the center of the mode plane is smaller than the center of the bend.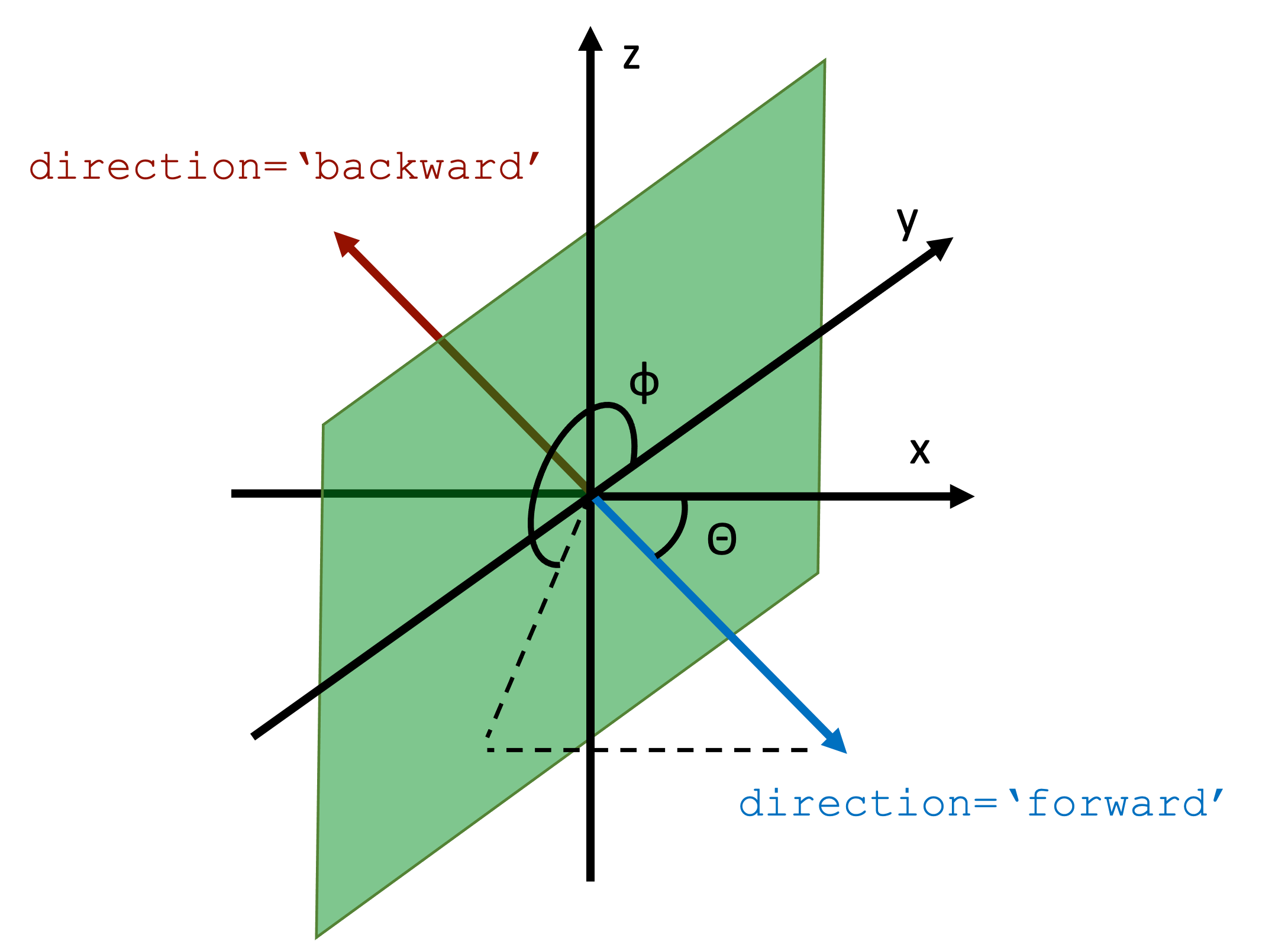

Example

>>> mode_spec = ModeSpec(num_modes=3, target_neff=1.5)

See also

Notebooks:

• Introduction on tidy3d working principles

• Defining mode sources and monitors

• Injecting modes in bent and angled waveguides

• Waveguide to ring coupling

Attributes

Methods

assign_default_on_true(val)	Assign the default fractional frequency step value if not provided.
bend_axis_given(val, values)	Check that bend_axis is provided if bend_radius is not None
bend_radius_not_zero(val, values)	Check that bend_raidus magnitude is not close to zero.`
check_group_step_size(val)	Ensure a reasonable group index step is used.
check_precision(values)	Verify critical ModeSpec settings for group index calculation.
glancing_incidence(val)	Warn if close to glancing incidence.

num_modes

target_neff

num_pml

filter_pol

angle_theta

angle_phi

precision

bend_radius

bend_axis

track_freq

group_index_step

classmethod bend_axis_given(val, values)

Check that bend_axis is provided if bend_radius is not None

classmethod bend_radius_not_zero(val, values)

Check that bend_raidus magnitude is not close to zero.`

classmethod glancing_incidence(val)

Warn if close to glancing incidence.

classmethod assign_default_on_true(val)

Assign the default fractional frequency step value if not provided.

classmethod check_group_step_size(val)

Ensure a reasonable group index step is used.

classmethod check_precision(values)

Verify critical ModeSpec settings for group index calculation.

__hash__()

Hash method.