Non-Dimensionalization and Integrated Loads Post-Processing in Flow360
Contents
7.2. Non-Dimensionalization and Integrated Loads Post-Processing in Flow360#
7.2.1. Introduction#
The main purpose of this tutorial is to provide a hands-on example for nondimensional inputs and outputs in Flow360. The tutorial includes running CFD cases with different
the CRM wing-body used during the 7th Drag Prediction Workshop
the XV-15 rotor blade using a time-accurate solution
the XV-15 rotor blade using a blade element theory (BET) disk solution
Note
Any value presented here in symbolic format (for example geometry->refArea) refers to a nondimensional value that is an input to the Flow360.json file.
7.2.2. Flow360 json file input calculations#
Firstly, the Flow360 json file input calculations are demonstrated for three different cases using different
Mesh Unit Length |
|
|---|---|
metres [m] |
1.0 m |
millimetres [mm] |
1 mm = 0.001 m |
feet [ft] |
1 ft = 0.3048 m |
inches [in] |
1 in = 0.0254 m |
unit chords [c=1.0] |
1 c_ref = (value of c_ref in metres) |
Typically for CFD studies, the user will either be given a Reynolds number directly from experimental data, or the value will have to be calculated. The Reynolds number can be calculated using the following equation, with the
7.2.2.1. CRM Wing-Body#
The CRM Wing-Body configuration has been used for the 7th Drag Prediction Workshop. The nominal flow conditions quoted on the 7th Drag Prediction Workshop website are a freestream Mach number of 0.85 and Reynolds number of
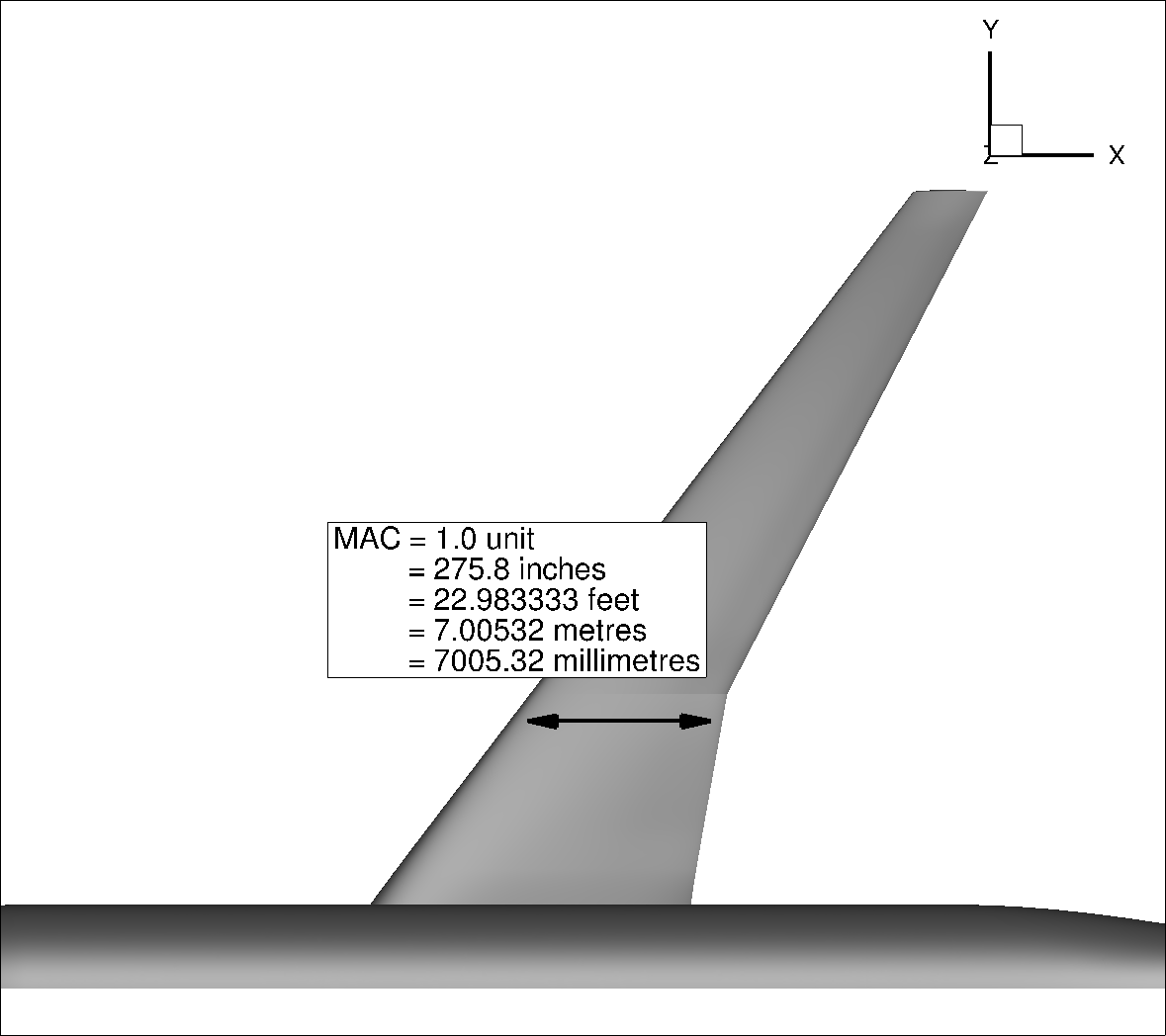
Fig. 7.2.1 CRM geometry scaled to different geometry and mesh units#
The calculation of the required inputs for the Flow360 json file, including the Reynolds number (using Eq.(7.2.1)), Flow360.json reference length (geometry->momentLength) and area (geometry->refArea) as well as the Mach number is presented in Table 7.2.2. The Flow360.json reference length is the nondimensional CRM wing MAC whereas the reference area is the nondimensional CRM wing area, with the dimensional values available here
MAC Unit |
Unit Chord |
Inches |
Feet |
Metres |
Millimetres |
|---|---|---|---|---|---|
|
|||||
|
|||||
|
|||||
|
0.85 |
0.85 |
0.85 |
0.85 |
0.85 |
The CFD calculation Reynolds number depends on the units used in the mesh due to the presence of a length component in the Reynolds number definition as seen in Eq.(7.2.1). The Flow360.json reference length (geometry->momentLength) and area (geometry->refArea) can be any value but will typically be the wing MAC and wing area nondimensionalized by
7.2.2.2. XV-15 Time-accurate and BET Disk#
The second example is the XV-15 rotor blade in both time-accurate and BET disk configurations. The reference data used in this example is available in this paper. Here the key parameters are the blade tip Mach number of 0.69, Reynolds number of
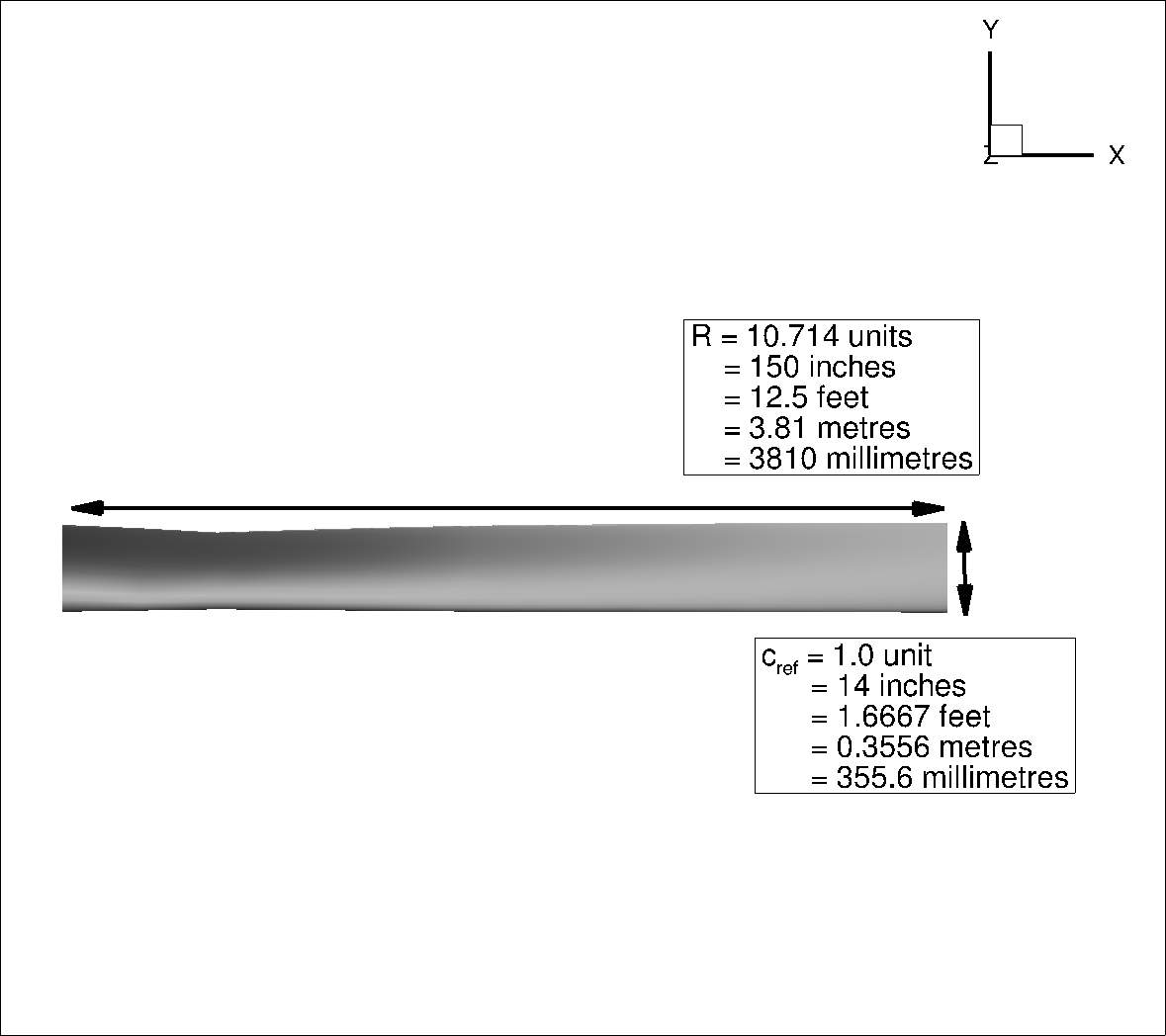
Fig. 7.2.2 XV-15 geometry scaled to different geometry and mesh units#
The calculation of the required inputs for the Flow360 json file, including the Reynolds number, Flow360.json reference length (geometry->momentLength) and area (geometry->refArea) as well as the Mach number (Mach) is presented in Table 7.2.3. Here, the reference length (geometry->momentLength) is the rotor radius nondimensionalized by the geometry->refArea) is the rotor disk area nondimensionalized by
The time step is nondimensionalized using the
For the XV-15 example, once again the CFD Reynolds input depends on the mesh units. For rotor calculations, the dimensional rotor radius and rotor disk area are scaled by the geometry->momentLength) and area (geometry->refArea) respectively. The input Mach number (Mach) is the freestream Mach number and is zero in this case, but a reference blade tip Mach number (MachRef) of 0.69 is used for scaling forces and moments. In this case, the nondimensional omega and time step size also depend on the mesh unit. For time marching rotor solutions, the simulation is typically initialized using a 1st order solution to establish the flowfield, and then continued using the 2nd order solver (see Knowledge Base). The 1st order initial solution Flow360.json and 2nd order solution Flow360.json files are available, with meters used as the mesh unit. For the BET simulation, an example Flow360.json file is also available, with inches used as the mesh unit.
MAC Unit |
Unit Chord |
Inches |
Feet |
Metres |
Millimetres |
|---|---|---|---|---|---|
|
|||||
|
|||||
|
|||||
|
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|
0.69 |
0.69 |
0.69 |
0.69 |
0.69 |
|
|||||
Time step per 1 degree |
7.2.3. Force and Moments Output Conventions#
For the steady CRM wing-body and time-marching XV15 rotor calculations, the forces and moments are output in nondimensional coefficients independent of the mesh unit. The total forces for all non-slip walls present in the calculation are stored in total_forces_v2.csv, whereas the forces on the individual non-slip walls are stored in surface_forces_v2.csv. For the BET calculation, the forces are also given in nondimensional form, but their values are scaled differently and are dependent on the mesh units used. The forces are stored in bet_forces_v2.csv. Firstly, the forces convention is presented for the steady CRM wing-body case and time-marching XV-15 rotor case, and following, the conventions for the BET forces are presented in more detail.
The typical output available in the WebUI and various csv files is outlined in Table 7.2.4. The conventions assume z-axis upwards, y-axis spanwise (+ towards starboard side) and x-axis in the axial direction (+ in the freestream direction) for the global axes, as shown in Fig. 7.2.3 for the example of the CRM wing-body. For steady simulations, the body axes are typically aligned with the global axes. The
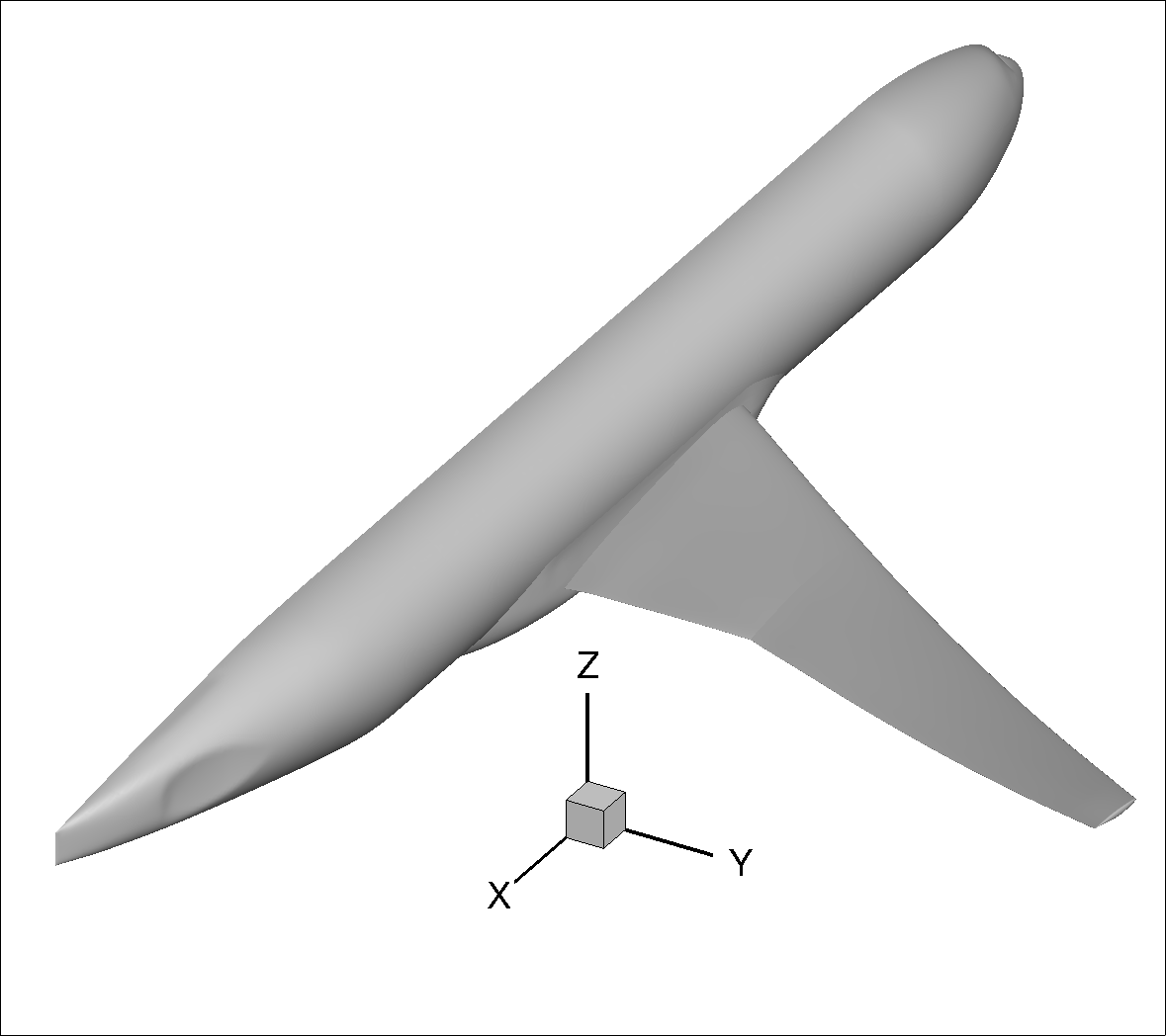
Fig. 7.2.3 Axis conventions demonstrated using the CRM geometry#
File |
Output |
|
|---|---|---|
total_forces_v2.csv, surface_forces_v2.csv and WebUI |
Force coefficients (global axes) |
|
-||- |
Moment coefficients (global axes) |
|
-||- |
Lift coefficient (wind axes) |
|
-||- |
Drag coefficient (wind axes) |
|
Not available (calculate from body forces) |
Side force coefficient (wind axes) |
|
total_forces_v2.csv, surface_forces_v2.csv |
Pressure contributions to force coefficients (global axes) |
|
-||- |
Pressure contributions to moment coefficients (global axes) |
|
-||- |
Skin friction contributions to force coefficients (global axes) |
|
-||- |
Skin friction contributions to moment coefficients (global axes) |
|
-||- |
Pressure contributions to the lift and drag coefficients |
|
-||- |
Skin friction contributions to the lift and drag coefficients |
|
bet_forces_v2.csv |
BET Disk nondimensional forces (global axes) |
|
-||- |
BET Disk nondimensional moments (global axes) |
The BET disk forces and moments are calculated based on the global coordinate system (inertial reference frame). The BET disk moments are based on the center of rotation and rotor radius of each BET disk. The nondimensional factors used for the forces and moments are explained in more detail in the following sections.
7.2.3.1. CRM Wing-Body#
For the CRM wing body, the output coefficient values are averaged over the last 10% steps (500 iterations). The output coefficient values are shown in Table 7.2.5, with the pitching moment coefficient being equivalent to CMy in this case. The lift and pitching moment coefficients can be converted into dimensional units using the following equations:
Coefficient |
Value |
|---|---|
0.6056 |
|
-0.12462 |
An example of converting the lift and pitching moment coefficients (other forces and moments are equivalent) into dimensional units is shown in Table 7.2.6 for a number of different mesh units following the equations above.
Units |
Lift |
Moment |
|---|---|---|
Unit Chord |
||
Inches |
||
Feet |
||
Metres |
||
Millimetres |
As can be seen from the example above, the coefficient values are independent of the mesh units used. When converting to dimensional forces, the product of the nondimensional reference area (geometry->refArea) and geometry->refArea), nondimensional reference length (geometry->momentLength) and
Note
When simulating a semi span airplane (like we have done above) the reference area must be properly set. If we want to get the forces on the whole aircraft from the semi span coefficients we should multiply the semi span refArea by 2.
7.2.3.2. Time-marching XV-15 Rotor Blade#
The example of the time-marching XV-15 rotor blade is not significantly different from the CRM wing-body case. In this case, the forces and moments are typically averaged over a revolution or number of revolutions (2 revolutions used here). As the rotor is in hover with the z-axis pointing upwards, the CFz value represents the thrust coefficient, whereas the CMz value represents the torque coefficient (note a 0.5 is used here in the denominator which is according to UK conventions). The resulting thrust and torque coefficients (CFz and CMz) are shown in Table 7.2.7. In this case, the rotor thrust and torque can be obtained using the following equations:
Coefficient |
Value |
|---|---|
CFz |
0.017001 |
CMz |
0.001955 |
As mentioned previously, the primary difference between fixed-wing and rotor calculations, is the fact that for rotor calculations, the nondimensional reference area (geometry->refArea) is typically taken as the rotor disk area scaled by geometry->momentLength). Here, since the freestream velocity is zero then the Mach is also zero. We thus use the blade tip Mach number as the reference Mach number. An example of obtaining the dimensional thrust and torque values for a number of units is shown in Table 7.2.8. Similarly as for the CRM wing-body example, the coefficient values are independent of the mesh units used.
Units |
Thrust |
Torque |
|---|---|---|
Unit Chord |
||
Inches |
||
Feet |
||
Metres |
||
Millimetres |
||
7.2.3.3. BET Disk XV-15 Rotor Blade#
The conversion of the forces and moments from the BET Disks is slightly different as the values are independent of the reference area and length specified in the Flow360.json file. This means that the nondimensional force and moment outputs in bet_forces_v2.csv vary depending on the mesh unit used. The dimensional thrust and torque values can be obtained using the following equations (assuming the rotor disk is aligned with z-axis pointing upwards):
The values obtained from the BET simulation using different mesh units for the Disk nondimensional z-force and moment about the z-axis are shown in Table 7.2.9
Unit |
Disk_Force_z |
Disk_Moment_z |
|---|---|---|
Unit Chords |
1.4073 |
1.1510 |
Inches |
275.8400 |
3158.2089 |
Feet |
1.9156 |
1.8277 |
Metres |
0.1780 |
0.0518 |
Millimetres |
177960.9339 |
51753770.9889 |
In this case, the nondimensional thrust and torque values vary with the mesh units used, however, all simulations lead to the same dimensional forces and moments. An example of obtaining the dimensional thrust and torque values for a number of units is shown in Table 7.2.10.
Units |
Thrust |
Torque |
|---|---|---|
Unit Chord |
||
Inches |
||
Feet |
||
Metres |
||
Millimetres |
This completes the tutorial on nondimensionalization conventions in Flow360. A short note on the results can be made, comparing results between the XV-15 time-marching and BET disk simulations. The dimensional thrust shows good agreement, however, the BET disk simulation predicts a much lower torque than the time-marching simulation. This is primarily due to the fact that very coarse grids were used in these simulations, hence the boundary layer is not well resolved for the time-marching simulation. The main purpose of this tutorial was to demonstrate the different nondimensionalization conventions used in Flow360.