Inverse design quickstart

This notebook will get users up and running with a very simple inverse design optimization with tidy3d. Inverse design uses the “adjoint method” to compute gradients of a figure of merit with respect to design parameters using only 2 simulations no matter how many design parameters are present. This gradient is then used to do high dimensional, gradient-based optimization of the system.

The setup we’ll demonstrate here involves a point dipole source and a point field monitor on either side of a dielectric box. Using the adjoint plugin in tidy3d, we use gradient-based optimization to maximize the intensity enhancement at the measurement spot with respect to the box size in all 3 dimensions.

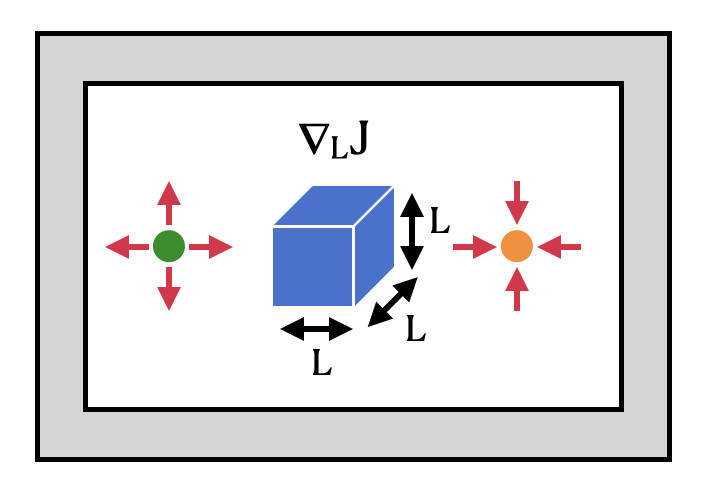
For more detailed notebooks, see these

• Tidy3D Adjoint Tutorial.

• Topology Optimization.

• Shape Optimization.

• Grating Coupler Inverse Design.

# To install tidy3d and the other packages needed, uncomment lines below.
# !pip install "tidy3d[jax]"
# !pip install optax

import tidy3d as td
import tidy3d.plugins.adjoint as tda
import matplotlib.pylab as plt

import jax
import jax.numpy as jnp
import optax

Setup

First, we set up some basic parameters and “static” components of our simulation.

# wavelength and frequency
wavelength = 1.55
freq0 = td.C_0 / wavelength

# permittivity of box
eps_box = 2

# size of sim in x,y,z
L = 10 * wavelength

# spc between sources, monitors, and PML / box
buffer = 1.0 * wavelength

# create a source to the left of sim
source = td.PointDipole(
    center=(-L/2 + buffer, 0, 0),
    source_time=td.GaussianPulse(freq0=freq0, fwidth=freq0 / 10.0),
    polarization="Ez",
)

# create a monitor to right of sim for measuring intensity
monitor = td.FieldMonitor(
    center=(+L/2 - buffer, 0, 0),
    size=(0, 0, 0),
    freqs=[freq0],
    name="point",
    colocate=False,
)

# create "base" simulation (the box will be added inside of the objective function later)
sim = tda.JaxSimulation(
    size=(L, L, L),
    grid_spec=td.GridSpec.auto(min_steps_per_wvl=25),
    structures=[],
    sources=[source],
    output_monitors=[monitor],
    monitors=[],
    run_time=120/freq0,
)

Define objective function

Now we construct our objective function out of some helper functions. Our objective function measures the intensity enhancement at the measurement point as a function of a design parameter that controls the box size.

# function to get box size (um) as a function of the design parameter (-inf, inf)

size_min = 0
size_max = L - 4 * buffer

def get_size(param: float):
    """Size of box as function of parameter, smoothly maps (-inf, inf) to (size_min, size_max)."""
    param_01 = 0.5 * (jnp.tanh(param) + 1)
    return (size_max * param_01) + (size_min * (1 - param_01))

# function to construct the simulation as a function of the design parameter

def make_sim(param: float) -> float:
    """Make simulation with a Box added, as given by the design parameter."""

    # for normalization, ignore any structures and return base sim
    if param is None:
        return sim.copy()

    # make a Box with the side length set by the parameter
    size_box = get_size(param)

    box = tda.JaxStructure(
        geometry=tda.JaxBox(
            center=(0, 0, 0),
            size=(size_box, size_box, size_box)
        ),
        medium=tda.JaxMedium(permittivity=eps_box)
    )

    # add the box to the simulation
    return sim.updated_copy(input_structures=[box])

# function to compute and measure intensity as function of the design paramater

def intensity(param: float) -> float:
    """Intensity measured at monitor as function of parameter."""

    # make the sim using the paramter value
    sim_with_square = make_sim(param)

    # run sim through tidy3d web API
    data = tda.web.run_local(sim_with_square, task_name="adjoint_quickstart", verbose=False)

    # evaluate the intensity at the measurement position
    return jnp.sum(jnp.array(data.get_intensity(monitor.name).values))

# get the intensity with no box, for normalization (care about enhancement, not abs value)
intensity_norm = intensity(param=None)
print(f"With no box, intensity = {intensity_norm:.4f}.")
print("This value will be used for normalization of the objective function.")

With no box, intensity = 95.8381.
This value will be used for normalization of the objective function.

def objective_fn(param: float) -> float:
    """Intensity at measurement point, normalized by intensity with no box."""
    return intensity(param) / intensity_norm

Optimization Loop

Next, we use jax to construct a function that returns the gradient of our objective function and use this to run our gradient-based optimization in a for loop.

# use jax to get function that returns objective function and its gradient
val_and_grad_fn = jax.value_and_grad(objective_fn)

# hyperparameters
num_steps = 9
learning_rate = 0.05

# initialize adam optimizer with starting parameter
param = -0.5
optimizer = optax.adam(learning_rate=learning_rate)
opt_state = optimizer.init(param)

# store history
objective_history = [1.0] # the normalized objective function with no box
param_history = [-100, param] # -100 is approximately "no box" (size=0)

for i in range(num_steps):
    print(f"step = {i + 1}")
    print(f"\tparam = {param:.4f}")
    print(f"\tsize = {get_size(param):.4f} um")

    # compute gradient and current objective funciton value
    value, gradient = val_and_grad_fn(param)

    # outputs
    print(f"\tintensity = {value:.4e}")
    print(f"\tgrad_norm = {jnp.linalg.norm(gradient):.4e}")

    # compute and apply updates to the optimizer based on gradient (-1 sign to maximize obj_fn)
    updates, opt_state = optimizer.update(-gradient, opt_state, param)
    param = optax.apply_updates(param, updates)

    # save history
    objective_history.append(value)
    param_history.append(param)

step = 1
        param = -0.5000
        size = 2.5012 um
        intensity = 5.9137e+00
        grad_norm = 1.3624e+00
step = 2
        param = -0.4500
        size = 2.6882 um
        intensity = 9.4693e+00
        grad_norm = 2.1216e+00
step = 3
        param = -0.4006
        size = 2.8809 um
        intensity = 1.1347e+01
        grad_norm = 1.9069e+00
step = 4
        param = -0.3509
        size = 3.0823 um
        intensity = 1.2976e+01
        grad_norm = 2.3161e+00
step = 5
        param = -0.3008
        size = 3.2919 um
        intensity = 1.6472e+01
        grad_norm = 4.8547e+00
step = 6
        param = -0.2531
        size = 3.4978 um
        intensity = 1.8129e+01
        grad_norm = 2.0547e+00
step = 7
        param = -0.2058
        size = 3.7064 um
        intensity = 1.7655e+01
        grad_norm = 2.4113e+00
step = 8
        param = -0.1583
        size = 3.9201 um
        intensity = 2.3258e+01
        grad_norm = 2.0198e+00
step = 9
        param = -0.1112
        size = 4.1351 um
        intensity = 2.2814e+01
        grad_norm = 3.2321e+00

Analysis

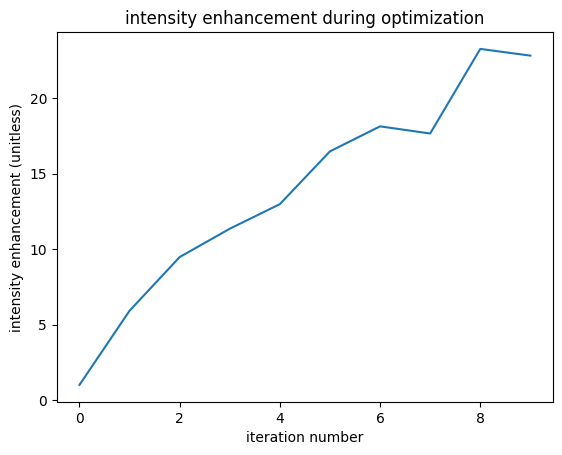
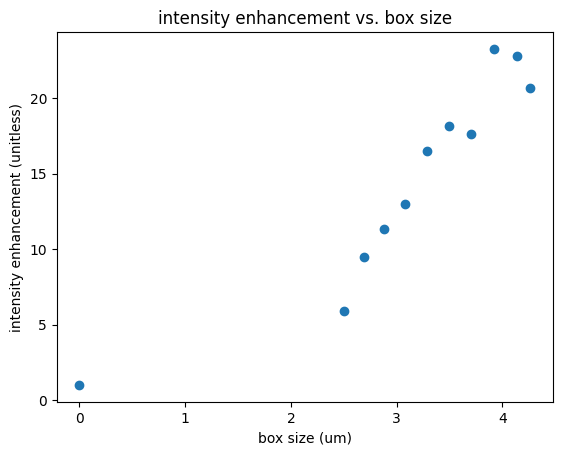
Finally we plot our results: optimization progress, field pattern, and box size vs intensity enhancement.

# objective function vs iteration number
plt.plot(objective_history)
plt.xlabel("iteration number")
plt.ylabel("intensity enhancement (unitless)")
plt.title("intensity enhancement during optimization")
plt.show()

# construct simulation with final parameters
sim_final = make_sim(param=param_history[-1])

# add a field monitor for plotting
fld_mnt = td.FieldMonitor(
    center=(+L/2 - buffer, 0, 0),
    size=(td.inf, td.inf, 0),
    freqs=[freq0],
    name="fields",
    colocate=False,
)
sim_final = sim_final.updated_copy(monitors=[fld_mnt])

# run simulation
data_final = tda.web.run_local(sim_final, task_name="quickstart_final", verbose=False)

# record final intensity
intensity_final = jnp.sum(jnp.array(data_final.get_intensity(monitor.name).values))
intensity_final_normalized = intensity_final / intensity_norm

objective_history.append(intensity_final_normalized)

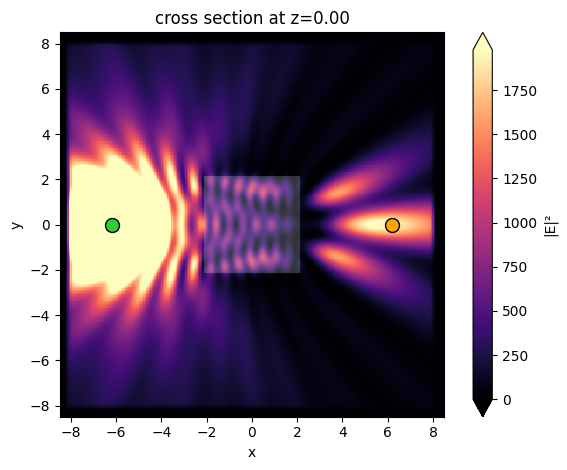
# plot intensity distribution
ax = data_final.plot_field(field_monitor_name="fields", field_name="E", val="abs^2", vmax=intensity_final)

ax.plot(source.center[0], 0, marker="o", mfc="limegreen", mec="black", ms=10)
ax.plot(monitor.center[0], 0, marker="o", mfc="orange", mec="black", ms=10)
plt.show()

# scatter the intensity enhancement vs the box size
sizes = [get_size(p) for p in param_history]
objective_history = objective_history
_ = plt.scatter(sizes, objective_history)
ax = plt.gca()
ax.set_xlabel('box size (um)')
ax.set_ylabel('intensity enhancement (unitless)')
plt.title('intensity enhancement vs. box size')
plt.show()