tidy3d.ModeSource#

class ModeSource[source]#

Bases: DirectionalSource, PlanarSource, BroadbandSource

Injects current source to excite modal profile on finite extent plane.

Parameters:

attrs (dict = {}) – Dictionary storing arbitrary metadata for a Tidy3D object. This dictionary can be freely used by the user for storing data without affecting the operation of Tidy3D as it is not used internally. Note that, unlike regular Tidy3D fields, attrs are mutable. For example, the following is allowed for setting an attr obj.attrs['foo'] = bar. Also note that Tidy3D` will raise a TypeError if attrs contain objects that can not be serialized. One can check if attrs are serializable by calling obj.json().
name (Optional[str] = None) – Optional name for the source.
center (Union[tuple[Union[float, autograd.tracer.Box], Union[float, autograd.tracer.Box], Union[float, autograd.tracer.Box]], Box] = (0.0, 0.0, 0.0)) – [units = um]. Center of object in x, y, and z.
size (Union[tuple[Union[pydantic.v1.types.NonNegativeFloat, autograd.tracer.Box], Union[pydantic.v1.types.NonNegativeFloat, autograd.tracer.Box], Union[pydantic.v1.types.NonNegativeFloat, autograd.tracer.Box]], Box]) – [units = um]. Size in x, y, and z directions.
source_time (Union[GaussianPulse, ContinuousWave, CustomSourceTime]) – Specification of the source time-dependence.
num_freqs (ConstrainedIntValue = 1) – Number of points used to approximate the frequency dependence of injected field. A Chebyshev interpolation is used, thus, only a small number of points, i.e., less than 20, is typically sufficient to obtain converged results.
direction (Literal['+', '-']) – Specifies propagation in the positive or negative direction of the injection axis.
mode_spec (ModeSpec = ModeSpec(attrs={}, num_modes=1, target_neff=None, num_pml=(0,, 0), filter_pol=None, angle_theta=0.0, angle_phi=0.0, precision='auto', bend_radius=None, bend_axis=None, bend_angle_rotation=False, track_freq='central', group_index_step=False, type='ModeSpec')) – Parameters to feed to mode solver which determine modes measured by monitor.
mode_index (NonNegativeInt = 0) – Index into the collection of modes returned by mode solver. Specifies which mode to inject using this source. If larger than mode_spec.num_modes, num_modes in the solver will be set to mode_index + 1.

Notes

Using this mode source, it is possible selectively excite one of the guided modes of a waveguide. This can be computed in our eigenmode solver tidy3d.plugins.mode.ModeSolver and implement the mode simulation in FDTD.

Mode sources are normalized to inject exactly 1W of power at the central frequency.

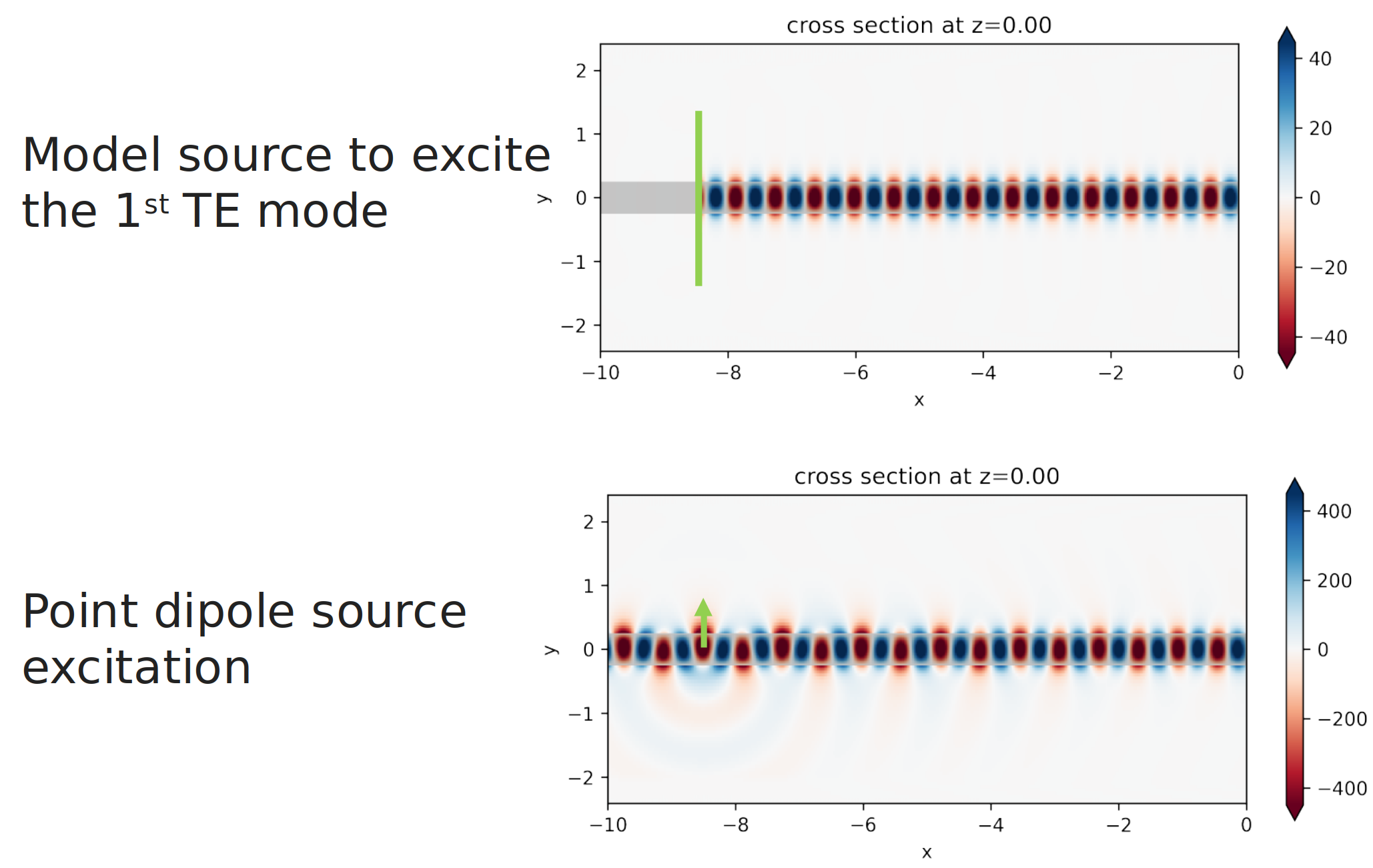
The modal source allows you to do directional excitation. Illustrated by the image below, the field is perfectly launched to the right of the source and there’s zero field to the left of the source. Now you can contrast the behavior of the modal source with that of a dipole source. If you just put a dipole into the waveguide, well, you see quite a bit different in the field distribution. First of all, the dipole source is not directional launching. It launches waves in both directions. The second is that the polarization of the dipole is set to selectively excite a TE mode. But it takes some propagation distance before the mode settles into a perfect TE mode profile. During this process, there is radiation into the substrate.

Example

>>> from tidy3d import GaussianPulse
>>> pulse = GaussianPulse(freq0=200e12, fwidth=20e12)
>>> mode_spec = ModeSpec(target_neff=2.)
>>> mode_source = ModeSource(
...     size=(10,10,0),
...     source_time=pulse,
...     mode_spec=mode_spec,
...     mode_index=1,
...     direction='-')

`angle_phi`	Azimuth angle of propagation.
`angle_theta`	Polar angle of propagation.
`attrs`

tidy3d.ModeSource

Contents

tidy3d.ModeSource#