Edge-mounted SMA to co-planar waveguide transition

Edge-mounted SMA to co-planar waveguide transition#

The subminiature version A (SMA) coaxial connector is an essential component in printed circuit board (PCB) applications. It is commonly used as the interface between the on-board circuit and external components such as antennas or measurement devices.

In this notebook, we model two edge-mounted SMA connectors attached to a grounded co-planar waveguide (CPW). The connector-to-connector insertion and return losses are calculated to ensure proper impedance matching and minimal reflection.

ed270fd2ea3a465089819b8d85d421ba

[1]:

import matplotlib.pyplot as plt
import numpy as np
import tidy3d as td
import tidy3d.plugins.microwave as mw
import tidy3d.plugins.smatrix as sm
from tidy3d import web

td.config.logging_level = "ERROR"

Building the Simulation#

Key Parameters#

[2]:

# Frequencies and bandwidth
(f_min, f_max) = (1e9, 10e9)
f0 = (f_min + f_max) / 2
freqs = np.linspace(f_min, f_max, 301)

Important geometry dimensions are defined below. The default length unit is microns, so we introduce a mm conversion factor.

[3]:

mm = 1000  # Conversion factor mm to microns

# Coaxial dimensions (50 ohm)
R0 = 0.635 * mm  # Coax inner radius
R1 = 2.125 * mm  # Coax outer radius

# Substrate overall dimensions
H = 1.57 * mm  # Substrate thickness
Lsub, Wsub = (83 * mm, 30 * mm)  # PCB board dimensions

# Transmission line dimensions
T = 0.038 * mm  #  Metal thickness
WS = 2.58 * mm  # Signal trace width
G = 1 * mm  # CPW gap width
WG = 5 * mm  # Side ground trace width

# Via dimensions
VR = 0.5 * mm  # Via radius
VP = 3 * mm  # Via pitch, longitudinal
VL = 3 * mm  # Via pitch, transverse
VS = 1 * mm  # Via start z-coordinate

# Edge mount dimensions
Voffset = 0.125 * mm  # SMA connector vertical offset

Medium and Structures#

Below, we define the materials used in model:

  • PTFE for the SMA dielectric core

  • Gold for the SMA body

  • FR4 for the PCB substrate

  • Copper for the PCB traces

[4]:

med_FR4 = td.Medium(permittivity=4.4)
med_PTFE = td.Medium(permittivity=2.1)
med_Cu = td.LossyMetalMedium(conductivity=60, frequency_range=(f_min, f_max))  # [S/um]
med_Au = td.LossyMetalMedium(conductivity=41, frequency_range=(f_min, f_max))  # [S/um]

The SMA geometry is imported from a STL file, and then translated and rotated to the appropriate position. The SMA core is created from a td.Cylinder instance. To ensure a close fit, we initialize the SMA core to be slightly larger than the inner radius and use Boolean subtraction to cut it to size.

[5]:

# Import SMA geometry
geom_SMA = td.TriangleMesh.from_stl(filename="./misc/SMA_model.stl", scale=mm, origin=(0, 0, 0))
geom_SMA = (geom_SMA.rotated(np.pi / 2, 0)).rotated(np.pi, 2)
geom_SMA = geom_SMA.translated(0, Voffset, 0)

# Create SMA dielectric core
geom_SMA_diel = td.Cylinder(
    center=(0, Voffset, -6 * mm / 2), radius=1.1 * R1, length=6 * mm, axis=2
)
geom_SMA_diel -= geom_SMA

We also make a copy for a second connector.

[6]:

# Make copy for second connector
geom_SMA2 = (geom_SMA.rotated(np.pi, 1)).translated(0, 0, Lsub)
geom_SMA_diel2 = (geom_SMA_diel.rotated(np.pi, 1)).translated(0, 0, Lsub)

The substrate and CPW geometries are created below.

[7]:

# Substrate
geom_sub = td.Box.from_bounds(rmin=(-Wsub / 2, -H - T, 0), rmax=(Wsub / 2, -T, Lsub))

# Transmission line and connecting structures
geom_sig = td.Box.from_bounds(rmin=(-WS / 2, -T, 0), rmax=(WS / 2, 0, Lsub))
geom_gnd1 = td.Box.from_bounds(rmin=(-WS / 2 - G - WG, -T, 0), rmax=(-WS / 2 - G, 0, Lsub))
geom_gnd2 = geom_gnd1.reflected((1, 0, 0))
geom_line = td.GeometryGroup(geometries=[geom_sig, geom_gnd1, geom_gnd2])
geom_gnd = td.Box.from_bounds(rmin=(-Wsub / 2, -H - 2 * T, 0), rmax=(Wsub / 2, -H - T, Lsub))

To ensure proper transmission in the high frequency range, we create a via fence that encloses the signal trace.

[8]:

# Create via fence
def create_via_hole(xpos, zpos):
    geom = td.Cylinder(center=(xpos, -H / 2 - T, zpos), axis=1, length=H, radius=VR)
    return geom


geom_via_array = []
zpos = VS
while zpos < Lsub - VS + 0.1 * mm:
    for xpos in [-VL, VL]:
        geom_via_array += [create_via_hole(xpos, zpos)]
    zpos += VP

geom_via_group = td.GeometryGroup(geometries=geom_via_array)

We combine the previously defined geometries and materials into Structure instances, ready for simulation.

[9]:

# Create structures
str_SMA = td.Structure(geometry=geom_SMA, medium=med_Au)
str_SMA2 = td.Structure(geometry=geom_SMA2, medium=med_Au)
str_SMA_diel = td.Structure(geometry=geom_SMA_diel, medium=med_PTFE)
str_SMA_diel2 = td.Structure(geometry=geom_SMA_diel2, medium=med_PTFE)
str_sub = td.Structure(geometry=geom_sub, medium=med_FR4)
str_line = td.Structure(geometry=geom_line, medium=med_Cu)
str_gnd = td.Structure(geometry=geom_gnd, medium=med_Cu)
str_vias = td.Structure(geometry=geom_via_group, medium=med_Cu)

# List of all structures
structure_list = [
    str_SMA,
    str_SMA2,
    str_SMA_diel,
    str_SMA_diel2,
    str_sub,
    str_line,
    str_gnd,
    str_vias,
]

Grid and Boundaries#

The simulation boundaries are open (PML) on all sides. We introduce a padding of wavelength/2 on all sides to ensure that the external boundaries do not encroach on the near-field.

[10]:

# Define simulation size and center
padding = td.C_0 / f0 / 2
sim_LZ = Lsub + padding
sim_LX = Wsub + padding
sim_LY = 5 * mm + padding
sim_center = (0, 0, Lsub / 2)

The grid refinement strategy is as follows:

  • Use LayerRefinementSpec for PCB metallic layers

  • Use MeshOverrideStructure for SMA dielectric core and metal via fences

[11]:

# Define layer refinement spec
lr_options = {
    "corner_refinement": td.GridRefinement(dl=0.1 * mm, num_cells=2),
    "min_steps_along_axis": 1,
}
lr1 = td.LayerRefinementSpec.from_structures(structures=[str_line], **lr_options)
lr2 = td.LayerRefinementSpec.from_structures(structures=[str_gnd], **lr_options)

# Define mesh override around SMA core and vias
rbox1 = td.MeshOverrideStructure(
    geometry=geom_SMA_diel.bounding_box, dl=(0.2 * mm, 0.2 * mm, 0.2 * mm)
)
rbox2 = td.MeshOverrideStructure(
    geometry=geom_SMA_diel2.bounding_box, dl=(0.2 * mm, 0.2 * mm, 0.2 * mm)
)
rbox_vias = []
for geom in geom_via_array:
    rbox_vias += [
        td.MeshOverrideStructure(geometry=geom.bounding_box, dl=(0.3 * mm, None, 0.3 * mm))
    ]

The overall grid specification is defined below.

[12]:

# Define overall grid specification
grid_spec = td.GridSpec.auto(
    min_steps_per_wvl=12,
    wavelength=td.C_0 / f_max,
    layer_refinement_specs=[lr1, lr2],
    override_structures=[rbox1, rbox2] + rbox_vias,
)

Monitors#

We define some field monitors for visualization purposes below.

[13]:

# Field Monitor
mon_1 = td.FieldMonitor(
    center=(0, -T - H / 2, 0),
    size=(td.inf, 0, td.inf),
    freqs=[f_min, f0, f_max],
    name="field in-plane",
)
mon_2 = td.FieldMonitor(
    center=(0, 0, 0),
    size=(0, td.inf, td.inf),
    freqs=[f_min, f0, f_max],
    name="field cross section",
)

# List of all monitors
monitor_list = [mon_1, mon_2]

Ports#

Wave ports are positioned along the coaxial section of each SMA connector.

[14]:

# Wave port position and dimension
wp_offset = 4 * mm  # longitudinal offset
w_port = 8 * mm  # port width and height

# Current integral for port impedance calculation
I_int = mw.CurrentIntegralAxisAligned(
    center=(0, Voffset, -wp_offset), size=(R0 + R1, R0 + R1, 0), sign="+"
)

# Define wave ports
WP1 = sm.WavePort(
    center=(0, Voffset, -wp_offset),
    size=(w_port, w_port, 0),
    mode_spec=td.ModeSpec(target_neff=np.sqrt(2.1)),
    direction="+",
    name="WP1",
    current_integral=I_int,
    frame=None,
)
WP2 = WP1.updated_copy(
    center=(0, Voffset, Lsub + wp_offset),
    direction="-",
    name="WP2",
    current_integral=I_int.updated_copy(center=(0, Voffset, Lsub + wp_offset), sign="-"),
)

Defining Simulation and TerminalComponentModeler#

The Simulation and TerminalComponentModeler instances are defined below.

[15]:

sim = td.Simulation(
    center=sim_center,
    size=(sim_LX, sim_LY, sim_LZ),
    grid_spec=grid_spec,
    structures=structure_list,
    monitors=monitor_list,
    run_time=5e-9,
    plot_length_units="mm",
    symmetry=(1, 0, 0),
)

tcm = sm.TerminalComponentModeler(
    simulation=sim,
    ports=[WP1, WP2],
    freqs=freqs,
)

Visualization#

Before running, it is a good idea to check the structure layout and simulation grid. Below, the top and side cross-sections of the structure is shown, along with the wave ports sources (green arrow) and internal modal absorbers (blue arrow).

[16]:

fig, ax = plt.subplots(1, 2, figsize=(10, 10), tight_layout=True)
tcm.plot_sim(
    y=-T, ax=ax[0], monitor_alpha=0, hlim=(-20 * mm, 20 * mm), vlim=(-15 * mm, Lsub + 15 * mm)
)
tcm.plot_sim(
    x=0, ax=ax[1], monitor_alpha=0, hlim=(-10 * mm, 10 * mm), vlim=(-15 * mm, Lsub + 15 * mm)
)
plt.show()
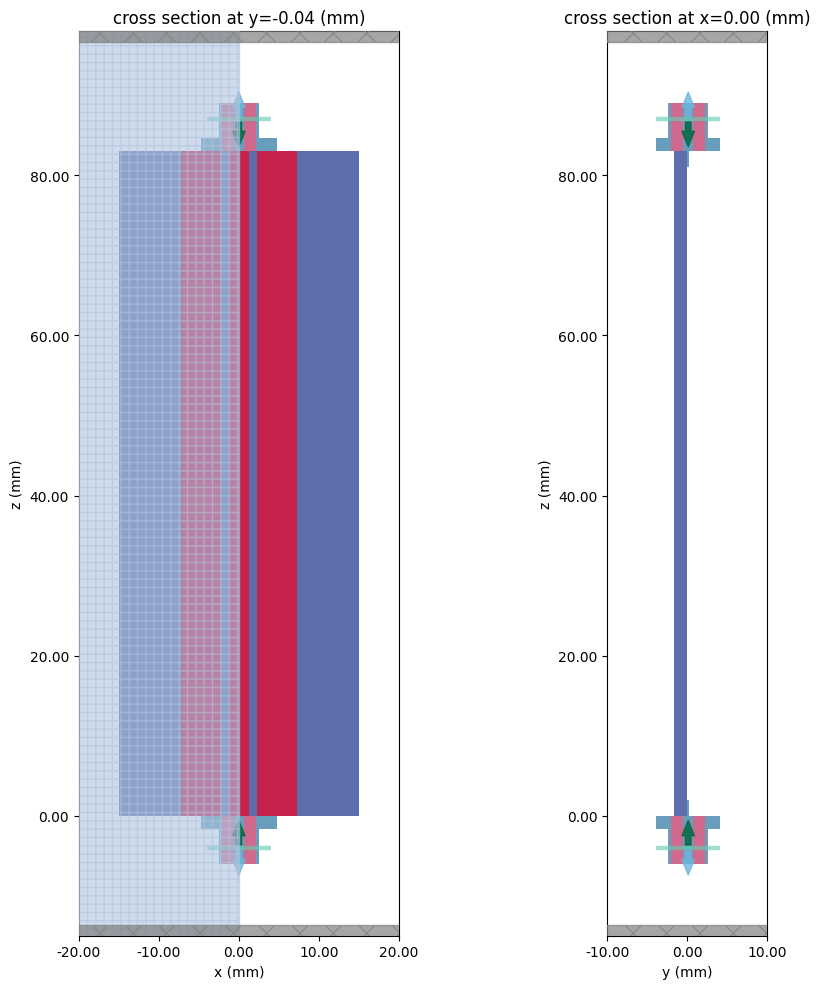
../_images/notebooks_SMAEdgeMount_40_0.png

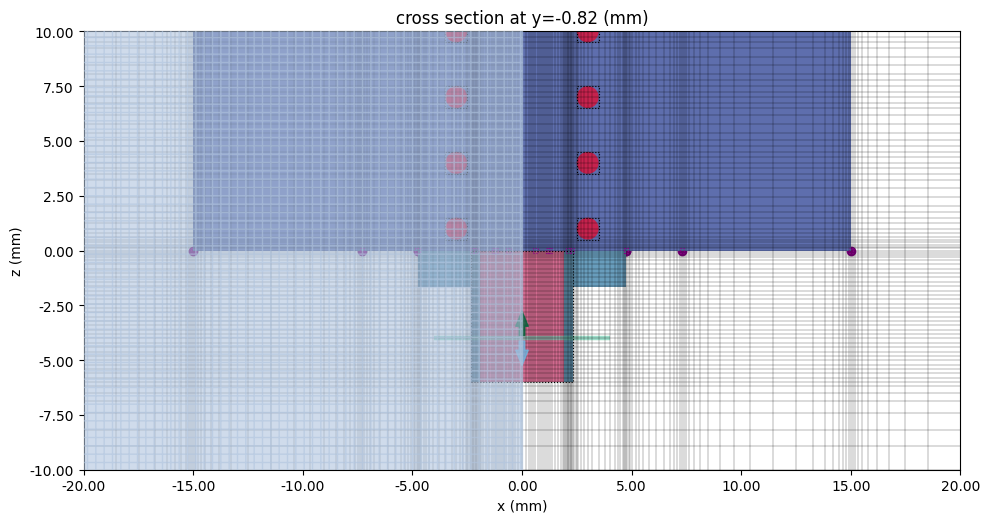
The grid in the SMA-CPW transition region is shown below. The mesh override regions are boxed with dotted black lines.

[17]:

fig, ax = plt.subplots(figsize=(10, 10), tight_layout=True)
tcm.simulation.plot_grid(y=-T - H / 2, ax=ax)
tcm.plot_sim(
    y=-T - H / 2, ax=ax, monitor_alpha=0, hlim=(-20 * mm, 20 * mm), vlim=(-10 * mm, 10 * mm)
)
plt.show()
../_images/notebooks_SMAEdgeMount_42_0.png

We can also visualize the setup in 3D.

[18]:

sim.plot_3d()

Running the Simulation#

The simulation is executed below.

[19]:

tcm_data = web.run(tcm, task_name="sma_connector", path="data/sma_connector.hdf5")

14:18:27 EDT Created task 'sma_connector' with resource_id
             'sid-7d07b37a-6775-426c-bdf3-0aa77befce63' and task_type 'RF'.

             View task using web UI at
             'https://tidy3d.simulation.cloud/rf?taskId=pa-4b736473-5db4-4765-a6
             50-d31032d7773b'.

             Task folder: 'default'.













14:18:31 EDT Child simulation subtasks are being uploaded to
             - WP2@0: 'rf-b83af70a-a477-43f4-9b93-d1c9fb469f97'
             - WP1@0: 'rf-3fa4cc77-df2a-4d9e-9afb-d852c9f84238'













14:18:33 EDT Validating component modeler and subtask simulations...













             Maximum FlexCredit cost: 0.461. Minimum cost depends on task
             execution details. Use 'web.real_cost(task_id)' to get the billed
             FlexCredit cost after a simulation run.













             Component modeler batch validation has been successful.













14:18:34 EDT Subtasks status - sma_connector
             Group ID: 'pa-4b736473-5db4-4765-a650-d31032d7773b'

























14:22:30 EDT Modeler has finished running successfully.













14:22:31 EDT Billed FlexCredit cost: 0.342. Minimum cost depends on task
             execution details. Use 'web.real_cost(task_id)' to get the billed
             FlexCredit cost after a simulation run.

















































14:23:06 EDT loading component modeler data from data/sma_connector.hdf5









Results#




Field Profile#


The field monitor data is accessed from the .data attribute of the TerminalComponentModelerData result. The key is in the format <wave port name>@<mode number>, for example WP1@0. (In this case, there is only one mode.)




[20]:





# Extract simulation data
sim_data = tcm_data.data["WP1@0"]







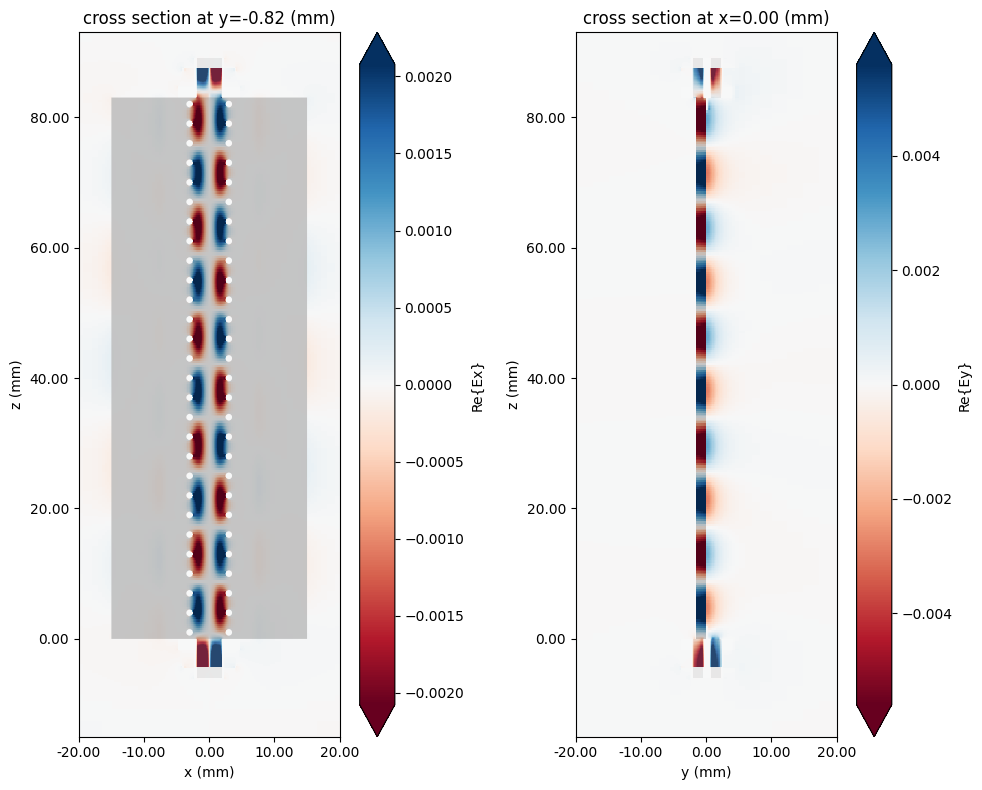
Below, the Ex and Ey field components are plotted along the top and side cross-sections respectively.




[21]:





fig, ax = plt.subplots(1, 2, figsize=(10, 8), tight_layout=True)
f_plot = f_max
sim_data.plot_field("field in-plane", field_name="Ex", val="real", f=f_plot, ax=ax[0])
sim_data.plot_field("field cross section", "Ey", val="real", f=f_plot, ax=ax[1])
for axis in ax:
    axis.set_ylim(-15 * mm, Lsub + 10 * mm)
    axis.set_xlim(-20 * mm, 20 * mm)
plt.show()














../_images/notebooks_SMAEdgeMount_53_0.png









S-parameters#


The S-matrix data is extracted using the smatrix() method. To access a specific S_ij parameter, use the corresponding port_in and port_out attributes. Note the use of np.conjugate to convert the S-parameter from the physics phase convention (current Tidy3D default) to the usual electrical engineering convention.




[22]:





# Extract S-matrix and S-parameters
smat = tcm_data.smatrix()
S11 = np.conjugate(smat.data.isel(port_in=0, port_out=0))
S21 = np.conjugate(smat.data.isel(port_in=0, port_out=1))







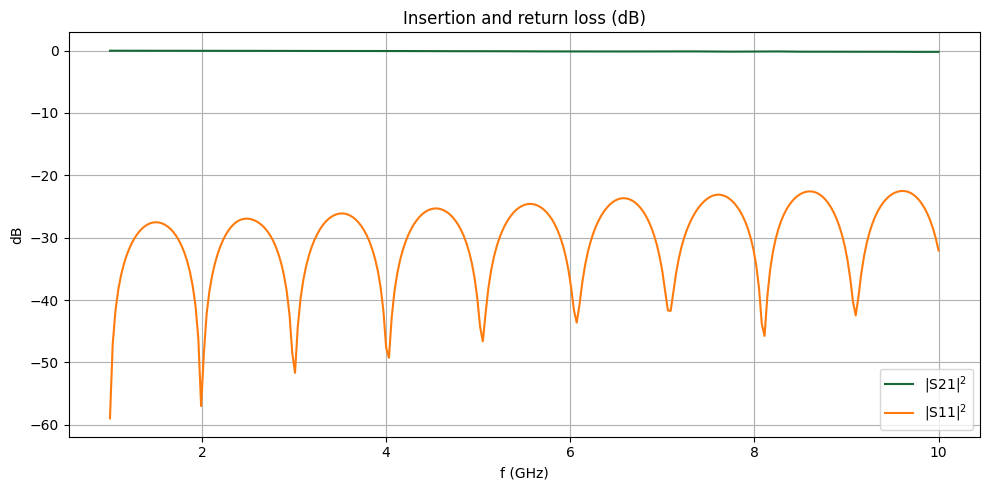
The insertion and return losses are plotted below. We observe excellent transmission and minimal reflection across the frequency band, indicating that the impedance of the SMA connector is well-matched to that of the on-board transmission line.




[23]:





fig, ax = plt.subplots(figsize=(10, 5), tight_layout=True)
ax.plot(freqs / 1e9, 20 * np.log10(np.abs(S21)), label="|S21|$^2$")
ax.plot(freqs / 1e9, 20 * np.log10(np.abs(S11)), label="|S11|$^2$")
ax.set_title("Insertion and return loss (dB)")
ax.set_xlabel("f (GHz)")
ax.set_ylabel("dB")
ax.legend()
ax.grid()
plt.show()














../_images/notebooks_SMAEdgeMount_58_0.png







[ ]:




















                

              

              
              
              
              
                
              
            

            
            
              
                



  

  

     Contents